题目内容
【题目】如图,在![]() 中,AB=AC,∠BAC=90
中,AB=AC,∠BAC=90![]() ,直角∠EPF的顶点是BC的中点,两边PE,PF分别交AB,AC于点E,F.给出以下五个结论:(1)AE=CF;(2)∠APE =∠CPF;(3)△EPF是等腰直角三角形;(4)
,直角∠EPF的顶点是BC的中点,两边PE,PF分别交AB,AC于点E,F.给出以下五个结论:(1)AE=CF;(2)∠APE =∠CPF;(3)△EPF是等腰直角三角形;(4)![]() =
=![]()
![]() (5)EF=AP其中一定成立的有________个.
(5)EF=AP其中一定成立的有________个.

【答案】4
【解析】
(1)通过证明△AEP≌△CFP就可以得出AE=CF,
(2)由∠EPA+∠FPA=90°,∠CPF+∠FPA=90°,就可以得出结论;
(3)由△AEP≌△CFP就可以PE=PF,即可得出结论;
(4)由S四边形AEPF=S△APE+S△APF.就可以得出S四边形AEPF=S△CPF+S△APF,就可以得出结论,
(5)由条件知AP=![]() BC,当EF是△ABC的中位线时才有EF=AP,其他情况EF≠AP.
BC,当EF是△ABC的中位线时才有EF=AP,其他情况EF≠AP.
(1)∵∠EPA+∠FPA=∠EPF=90°,∠CPF+∠FPA=90°,
∴∠APE=∠CPF,故(1)正确.
∵AB=AC,∠BAC=90°,
∴∠B=∠C=45°.
∵P是BC的中点,
∴BP=CP=AP=![]() BC.∠BAP=∠CAP=45°.
BC.∠BAP=∠CAP=45°.
∴.∠BAP=∠C.
在△AEP和△CFP中
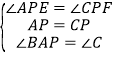 ,
,
∴△AEP≌△CFP(ASA),
∴AE=CF,PE=PF,S△AEP=S△CFP,故(2)正确.
∴△EPF是等腰直角三角形,故(3)正确.
∵S四边形AEPF=S△APE+S△APF.
∴S四边形AEPF=S△CPF+S△APF=S△APC=![]() S△ABC,故(4)正确.
S△ABC,故(4)正确.
∵△ABC是等腰直角三角形,P是BC的中点,
∴AP=![]() BC,
BC,
∵EF不是△ABC的中位线,
∴EF≠AP,故(5)错误;
∴正确的共有4个.
故答案为4.

 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案【题目】近期,我市中小学广泛开展了“传承中华文化,共筑精神家园”爱国主义读书教育活动,某中学为了解学生最喜爱的活动形式,以“我最喜爱的一种活动”为主题,进行随机抽样调查,收集数据整理后,绘制出以下两幅不完整的统计图表,请根据图中提供的信息,解答下面的问题:
最喜爱的一种活动统计表
活动形式 | 征文 | 讲故事 | 演讲 | 网上竞答 | 其他 |
人数 | 60 | 30 | 39 | a | b |

(1)在这次抽样调查中,一共调查了多少名学生?扇形统计图中“讲故事”部分的圆心角是多少度?
(2)如果这所中学共有学生3800名,那么请你估计最喜爱征文活动的学生人数.



