题目内容
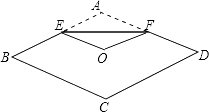
【题目】如图,在直角梯形ABCD中,AB∥CD,AD⊥DC,AB=BC,且AE⊥BC.
(1)求证:AD=AE;
(2)若AD=8,DC=4,求AB的长.
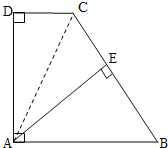
【答案】:解:(1)连接AC,
∵AB∥CD,
∴∠ACD=∠BAC,
∵AB=BC,
∴∠ACB=∠BAC,
∴∠ACD=∠ACB,
∵AD⊥DCAE⊥BC,
∴∠D=∠AEC=90°,
∵AC=AC,
∴△ADC≌△AEC,
∴AD=AE;
(2)由(1)知:AD=AE,DC=EC,
设AB=x,则BE=x﹣4,AE=8,
在Rt△ABE中∠AEB=90°,
由勾股定理得:82+(x﹣4)2=x2,
解得:x=10,
∴AB=10.
说明:依据此评分标准,其它方法如:过点C作CF⊥AB用来证明和计算均可得分.
【解析】:(1)连接AC,证明△ADC与△AEC全等即可;
(2)设AB=x,然后用x表示出BE,利用勾股定理得到有关x的方程,解得即可.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目