题目内容
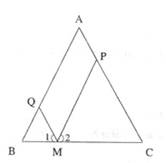
已知:在△ABC中,AB=AC=a,M为底边BC上的任意一点,过点M分别作AB、AC的平行线交AC于P,交AB于Q。
(1)求四边形AQMP的周长。
(2)写出图中的两对相似三角形(不需证明)。
(3)M位于BC的什么位置时,四边形AQMP为菱形?说明你的理由。

解:(1)∵PM//AB,QM//AC
∴四边形AQMP为平行四边形且∠1=∠2,∠2=∠B
又∵AB=AC=a
∴∠B=∠C ∴∠1=∠B=∠C=∠2
∴ QB=QM, PM=PC
∴四边形AQMP的周长为: AQ+QM+MP+PA=AQ+QB+PC+PA=AB+AC=2a
(2) △ABC∽△QBM∽△PMC(三对中写出任意两对即可)
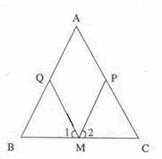
(3)当M为底边BC的中点时,四边形AQMP为菱形
当M为BC中点时
∵PM//AB, QM//AC
∴![]()
![]()
∴PM=QM
由(1)知:四边形AQMP为平行四边形
∴四边形AQMP为菱形

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
 25、已知:在△ABC中AB=AC,点D在CB的延长线上.
25、已知:在△ABC中AB=AC,点D在CB的延长线上. (1)化简:(a-
(1)化简:(a- 20、如图,已知,在△ABC中,∠ABC和∠ACB的平分线交于点M,ME∥AB交BC于点E,MF∥AC交BC于点F.求证:△MEF的周长等于BC的长.
20、如图,已知,在△ABC中,∠ABC和∠ACB的平分线交于点M,ME∥AB交BC于点E,MF∥AC交BC于点F.求证:△MEF的周长等于BC的长. 12、已知,在△ABC中,AB=AC=x,BC=6,则腰长x的取值范围是
12、已知,在△ABC中,AB=AC=x,BC=6,则腰长x的取值范围是
 已知:在△ABC中,∠B<∠C,AD平分∠BAC,AE⊥BC,垂足为点E.∠B=38°,∠C=70°.
已知:在△ABC中,∠B<∠C,AD平分∠BAC,AE⊥BC,垂足为点E.∠B=38°,∠C=70°.