��Ŀ����
����Ŀ������Rt��ACB����ACB��90�㣬AC��BC����A��C�ֱ���x�ᡢy����������ϣ�

��1����ͼ1����֤����BCO����CAO
��2����ͼ2����OA��5��OC��2����B�������
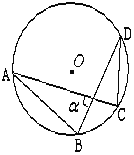
��3����ͼ3����C��0��3����Q��A�������x���ϣ���S��CQA��18���ֱ���AC��CQΪ���ڵ�һ���ڶ�����������Rt��CAN������Rt��QCM������MN��y����P�㣬OP�ij����Ƿ����ı䣿�����䣬���OP��ֵ�����仯����OP��ȡֵ��Χ��
���𰸡���1����������2������2����3����3��OP�ij��Ȳ��ᷢ���ı䣬9
��������
��1������ͬ�ǵ������ȵó����ۼ��ɣ�
��2���ȹ���B��BD��y����D�����ж���CDB�ա�AOC��AAS�������BD=CO=2��CD=AO=5�������ó�OD=5-2=3�����ɵõ�B������ꣻ
��3���ȹ�N��NH��CM����y����H������HCN�ա�QAC��ASA�����ó�CH=AQ��HN=QC��Ȼ����ݵ�C��0��3����S��CQA=18�����AQ=12������ж���PNH�ա�PMC��AAS�����ó�![]() ���������CP=3+6=9����ֵ����
���������CP=3+6=9����ֵ����
�⣺��1����ͼ1��

�ߡ�ACB��90������AOC��90����
���BCO+��ACO��90������CAO+��ACO��
���BCO����CAO��
��2����ͼ2������B��BD��y����D�����CDB����AOC��90����

����CDB����AOC��
 ��
��
���CDB�ա�AOC��AAS����
��BD��CO��2��CD��AO��5��
��OD��5��2��3��
�֡ߵ�B�ڵ������ޣ�
��B����2����3����
��3��OP�ij��Ȳ��ᷢ���ı䣮
���ɣ���ͼ3����N��NH��CM����y����H����

��CNH+��MCN��180����
�ߵ���Rt��CAN������Rt��QCM��
���MCQ+��ACN��180����
���ACQ+��MCN��360����180����180����
���CNH����ACQ��
�֡ߡ�HCN+��ACO��90������QAC+��ACO��
���HCN����QAC��
����HCN����QAC��
 ��
��
���HCN�ա�QAC��ASA����
��CH��AQ��HN��QC��
��QC��MC��
��HN��CM��
�ߵ�C��0��3����S��CQA��18��
��![]() ��AQ��CO��18����
��AQ��CO��18����![]() ��AQ��3��18��
��AQ��3��18��
��AQ��12��
��CH��12��
��NH��CM��
���PNH����PMC��
������PNH����PMC��
 ��
��
���PNH�ա�PMC��AAS����
��CP��PH��![]() CH��6��
CH��6��
�֡�CO��3��
��CP��3+6��9����ֵ����
��OP�ij���ʼ����9��

 ����˼ά�żӿ���ϵ�д�
����˼ά�żӿ���ϵ�д� �����Ծ�ϵ�д�
�����Ծ�ϵ�д�