题目内容
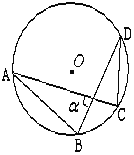
【题目】如图⊙O的半径为1cm,弦AB、CD的长度分别为![]() ,则弦AC、BD所夹的锐角
,则弦AC、BD所夹的锐角![]() = .
= .
【答案】75°.
【解析】试题分析:根据勾股定理的逆定理可证△AOB是等腰直角三角形,故可求∠OAB=∠OBA=45°,又由已知可证△COD是等边三角形,所以∠ODC=∠OCD=60°,根据圆周角的性质可证∠CDB=∠CAB,而∠ODB=∠OBD,所以∠CAB+∠OBD=∠CDB+∠ODB=∠ODC=60°,再根据三角形的内角和定理可求α.
解:连接OA、OB、OC、OD,
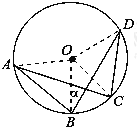
∵OA=OB=OC=OD=1,AB=![]() ,CD=1,
,CD=1,
∴OA2+OB2=AB2,
∴△AOB是等腰直角三角形,
△COD是等边三角形,
∴∠OAB=∠OBA=45°,∠ODC=∠OCD=60°,
∵∠CDB=∠CAB,∠ODB=∠OBD,
∴α=180°-∠CAB-∠OBA-∠OBD=180°-∠OBA-(∠CDB+∠ODB)=180°-45°-60°=75°.

练习册系列答案
相关题目