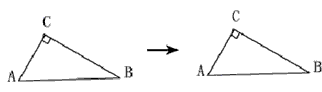Question

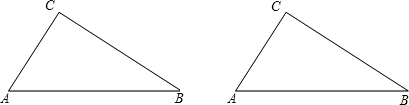
23、下图是一个三角形，已知∠ACB=90°，那么∠A的余角是

∠B

； 小明用三角尺在这个三角形中画了一条高CD（点D是垂足），得到右图：
（1）请你帮小明画出这条高；
（2）在下图中，小明通过观察、认真思考，找出了三对互余的角，你能帮小明把它们写出来吗？
答：①

∠A与∠ACD

；  ②

∠ACD与∠BCD

；    ③

∠B与∠BCD

．
（3）∠ACB、∠ADC、∠CDB都是直角，所以∠ACB=∠ADC=∠CDB，小明还发现了另外两对相等的角，请你也仔细地观察、认真地思考分析，试一试，能发现吗？把它们写出来，并请说明理由．

Answer 1

分析：根据互余的两个角的和等于90°解答：
（1）根据互余的两个角的和等于90°，∠A+∠ACD=90°，∠ACD+∠BCD=90°，∠B+∠BCD=90°；
（2）根据同角或等角的余角相等写出即可．

解答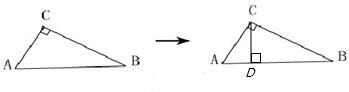：解：根据余角的定义，
∴∠A的余角是∠B，
故答案为：∠B；

（1）根据互余的两个角的和等于90°，
∴①∠A与∠ACD，②∠ACD与∠BCD，③∠B与∠BCD，
故答案为：①∠A与∠ACD，②∠ACD与∠BCD，③∠B与∠BCD；

（2）∠A=∠BCD，∠B=∠ACD．
证明：∵∠A+∠ACD=90°，∠ACD+∠BCD=90°，∠B+∠BCD=90°
根据同角的余角相等，
∴∠A=∠BCD，∠B=∠ACD．

点评：本题主要考查了：（1）余角的定义，如果两个角的和等于90°，那么这两个角互为余角；（2）同角或等角的余角相等，熟练掌握概念和性质是解题的关键，难度适中．