Question

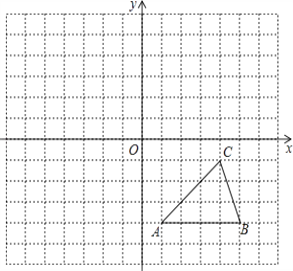
【题目】△ABC与△A′B′C′在平面直角坐标系中的位置如图

（1）分别写出下列各点的坐标：A′______；B′______；C′______

（2）若点P（m，n）是△ABC内部一点，则平移后△A′B′C′内的对应点P′的坐标为______．

（3）求△ABC的面积．

Answer 1

【答案】（1）A′（-3，-4），B′（0，-1），C′（2，-3）；（2）（m-4，n-4）；（3）△ABC的面积为=..

【解析】

（1）根据平面直角坐标系的特点直接写出坐标；

（2）首先根据A与A′的坐标观察变化规律，P的坐标变换与A点的变换一样，写出点P′的坐标；

（3）先求出△ABC所在的矩形的面积，然后减去△ABC四周的三角形的面积即可．

解：（1）如图所示：

A′（-3，-4），B′（0，-1）、C′（2，-3）；

（2）A（1，0）变换到点A′的坐标是（-3，-4），横坐标减4，纵坐标减4，

∴点P的对应点P′的坐标是（m-4，n-4）；

（3）△ABC的面积为：3×5-×2×5-×2×2-×3×3=．

故答案为：（-3，-4），（0，-1）、（2，-3）；（m-4，n-4）．