题目内容
 如图,⊙O的弦AB⊥AC,AB=AC,OM⊥AB,ON⊥AC,垂足分别为M、N,若AB=2,则⊙O的半径为________.
如图,⊙O的弦AB⊥AC,AB=AC,OM⊥AB,ON⊥AC,垂足分别为M、N,若AB=2,则⊙O的半径为________.

分析:根据垂径定理得出ON=OM,AM=BM=
 AB,AN=CN=
AB,AN=CN= AC,根据垂直定义得到∠A=∠OMA=∠ONA=90°,得出正方形OMAN,求出ON=CN=1,根据勾股定理即可求出答案.
AC,根据垂直定义得到∠A=∠OMA=∠ONA=90°,得出正方形OMAN,求出ON=CN=1,根据勾股定理即可求出答案.解答:
 解:如图,连接OC,
解:如图,连接OC,∵⊙O的弦AB=AC,OM⊥AB,ON⊥AC,
∴ON=OM,AM=BM=
 AB=1,AN=CN=
AB=1,AN=CN= AC=1,
AC=1,即:AN=AM,
∵OM⊥AB,ON⊥AC,AB⊥AC,
∴∠A=∠OMA=∠ONA=90°,
∴四边形OMAN是正方形,
∴ON=AN=1,
连接OC,
由勾股定理得:OC=
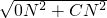 =
= .
.故答案为:
 .
.点评:本题主要考查对垂径定理,勾股定理,正方形的性质和判定,垂线的定义等知识点的理解和掌握,求出正方形OMAN是解此题的关键.

练习册系列答案
相关题目
 13、如图,⊙O的弦AB和CD相交于K,过弦AB、CD的两端的切线分别相交于P、Q,求证:OK⊥PQ.
13、如图,⊙O的弦AB和CD相交于K,过弦AB、CD的两端的切线分别相交于P、Q,求证:OK⊥PQ.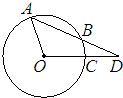 64、如图,⊙O的弦AB、半径OC延长交于点D,BD=OA,若∠AOC=105°,求∠D的度数.
64、如图,⊙O的弦AB、半径OC延长交于点D,BD=OA,若∠AOC=105°,求∠D的度数.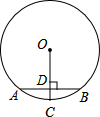 如图,⊙O的弦AB=10,OC⊥AB,且OD=12,则⊙O的半径等于( )
如图,⊙O的弦AB=10,OC⊥AB,且OD=12,则⊙O的半径等于( )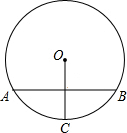 如图,⊙O的弦AB垂直平分半径OC,若AB=
如图,⊙O的弦AB垂直平分半径OC,若AB=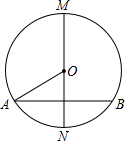 如图,⊙O的弦AB垂直于直径MN,C为垂足,若OA=5cm,CN=2cm,则AB=
如图,⊙O的弦AB垂直于直径MN,C为垂足,若OA=5cm,CN=2cm,则AB=