题目内容
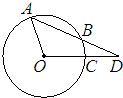 64、如图,⊙O的弦AB、半径OC延长交于点D,BD=OA,若∠AOC=105°,求∠D的度数.
64、如图,⊙O的弦AB、半径OC延长交于点D,BD=OA,若∠AOC=105°,求∠D的度数.分析:利用BD=AO=OB,结合等腰三角形的性质及内角和定理求解.
解答:解:连接OB,
∵BD=OA,OB=OA,
∴BD=AO=OB,
∴△OBD,△OAB都是等腰三角形,
设∠D的度数是x,
则利用三角形的内角得是180度,可得:
105-x+2x+2x=180,
解得x=25.
∵BD=OA,OB=OA,
∴BD=AO=OB,
∴△OBD,△OAB都是等腰三角形,
设∠D的度数是x,
则利用三角形的内角得是180度,可得:
105-x+2x+2x=180,
解得x=25.
点评:本题主要是利用等腰三角形和三角形的内角得定理理清角与角的关系,然后列方程求解即可.

练习册系列答案
相关题目
 13、如图,⊙O的弦AB和CD相交于K,过弦AB、CD的两端的切线分别相交于P、Q,求证:OK⊥PQ.
13、如图,⊙O的弦AB和CD相交于K,过弦AB、CD的两端的切线分别相交于P、Q,求证:OK⊥PQ.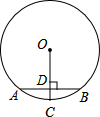 如图,⊙O的弦AB=10,OC⊥AB,且OD=12,则⊙O的半径等于( )
如图,⊙O的弦AB=10,OC⊥AB,且OD=12,则⊙O的半径等于( )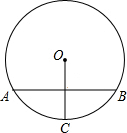 如图,⊙O的弦AB垂直平分半径OC,若AB=
如图,⊙O的弦AB垂直平分半径OC,若AB=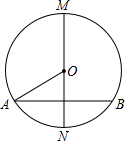 如图,⊙O的弦AB垂直于直径MN,C为垂足,若OA=5cm,CN=2cm,则AB=
如图,⊙O的弦AB垂直于直径MN,C为垂足,若OA=5cm,CN=2cm,则AB=