题目内容
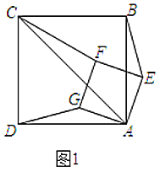
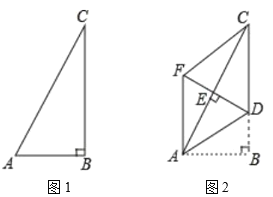
【题目】如图1,在![]() 中,
中,![]() ,
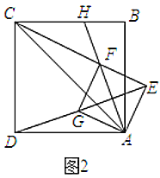
,![]() .如图2,将
.如图2,将![]() 向上翻折,使点
向上翻折,使点![]() 落在
落在![]() 上,记为点
上,记为点![]() ,折痕为
,折痕为![]() .过
.过![]() 点作
点作![]() 平行线交
平行线交![]() 延长线于点
延长线于点![]() ,连接
,连接![]() .
.
(1)证明:四边形![]() 是菱形.
是菱形.
(2)若![]() ,求
,求![]() 的长度.
的长度.
【答案】(1)见解析;(2)2![]()
【解析】
(1)利用含30度角的直角三角形的性质得到AC=2AB,利用翻折的性质得到AE=AB,DE⊥AC,再证明△AEF![]() △CED,EF=DE,根据对角线互相垂直平分的四边形是菱形即可证得结论;
△CED,EF=DE,根据对角线互相垂直平分的四边形是菱形即可证得结论;
(2)利用(1)的结论结合三角函数的知识,即可求得DE的长,从而求得DF的长度.
(1)在![]() 中,
中,![]() ,
,![]() .
.
∴AC=2AB,
由折叠的性质得:∠AED=∠B=90°,AE=AB,
∴AC⊥DF,
∵AC=2AB,
∴CE=AB=AE,
∵AF∥CD,
∴∠FAE=∠DCE,
在△AEF和△CED中,
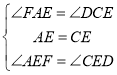 ,
,
∴△AEF![]() △CED,
△CED,
∴EF= ED,
又∵CE =AE,AC⊥DF,
∴四边形![]() 是菱形;
是菱形;
(2)由(1)得:AC=2AB=2 AE,
∴AE=3,
由折叠的性质得:∠EAD=∠BAD=![]() (90°-∠ACB)= 30°,
(90°-∠ACB)= 30°,
∵![]() ,即
,即![]() ,
,
∴DE=![]() ,
,
∴DF= 2DE=2![]() .
.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目