题目内容
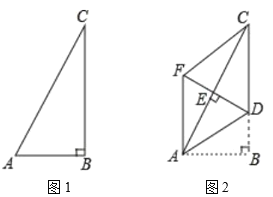
【题目】如图,在Rt△ACB中,∠ACB=90°,AC=BC,点D是AB上的一个动点(不与点A,B重合),连接CD,将CD绕点C顺时针旋转90°得到CE,连接DE,DE与AC相交于点F,连接AE,则图中与△ACE全等或相似的三角形有( )
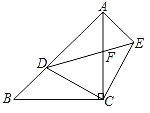
A.1个B.2个C.3个D.4个
【答案】C
【解析】
先证明△ACE≌△BCD,得∠CAE=∠CEF=45°,再证明△ACE∽△ECF,最后证明△ACE∽△ADF,便可得结论.
解:∵将CD绕点C顺时针旋转90°得到CE,
∴CE=CD,
∵∠ACB=∠DCE=90°,
∴∠BCD=∠ACE,
在△ACE和△BCD中,
 ,
,
∴△ACE≌△BCD(SAS);
∴∠CAE=∠B=45°,
∵CE=CD,∠DCE=90°
∴∠CEF=45°
∵∠ACE=∠ECF,
∴△ACE∽△ECF;
∵∠FAD=∠FEC=45°,∠AFD=∠EFC,
∴∠ADF=∠ACE,
∵∠DAF=∠CAE=45°,
∴△ACE∽△ADF,
综上,图中与△ACE全等或相似的三角形有3个.
故选:C.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】某校举行“诵读经典”朗诵比赛,把比赛成绩分为四个等次:![]() 优秀,
优秀,![]() .良好,
.良好,![]() .一般,
.一般,![]() .较差,从参加比赛的学生中随机抽取部分学生的成绩进行调查,并根据调查结果制作了如下的统计图表(不完整):
.较差,从参加比赛的学生中随机抽取部分学生的成绩进行调查,并根据调查结果制作了如下的统计图表(不完整):
学生朗读比赛成绩频数分布表
等次 | 频数 | 频率 |
|
| 0.1 |
| 20 | 0.4 |
|
|
|
| 10 | 0.2 |
合计 | 1 |
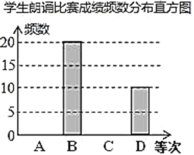
(1)这次共调查了______名学生,表中![]() _____,
_____,![]() _____,
_____,![]() _____;
_____;
(2)补全频数分布直方图;
(3)若抽查的学生中,等次![]() 中有2名女生,其他为男生,从等次
中有2名女生,其他为男生,从等次![]() 中选取两名同学参加市中学生朗诵比赛,求恰好选取一名男生和一名女生的概率.
中选取两名同学参加市中学生朗诵比赛,求恰好选取一名男生和一名女生的概率.