题目内容
【题目】已知圆E:(x+ ![]() )2+y2=16,点F(
)2+y2=16,点F( ![]() ,0),P是圆E上任意一点,线段PF的垂直平分线和半径PE相交于Q.(Ⅰ)求动点Q的轨迹E的方程; (Ⅱ)直线l过点(1,1),且与轨迹Γ交于A,B两点,点M满足
,0),P是圆E上任意一点,线段PF的垂直平分线和半径PE相交于Q.(Ⅰ)求动点Q的轨迹E的方程; (Ⅱ)直线l过点(1,1),且与轨迹Γ交于A,B两点,点M满足 ![]() =
= ![]() ,点O为坐标原点,延长线段OM与轨迹Γ交于点R,四边形OARB能否为平行四边形?若能,求出此时直线l的方程,若不能,说明理由.
,点O为坐标原点,延长线段OM与轨迹Γ交于点R,四边形OARB能否为平行四边形?若能,求出此时直线l的方程,若不能,说明理由.
【答案】解:(I)∵|QE|+|QF|=|EQ|+|QP|=4,且|EF|=2 ![]() <4, ∴点Q的轨迹是以E,F为焦点的椭圆,
<4, ∴点Q的轨迹是以E,F为焦点的椭圆,
设椭圆方程为 ![]() =1,则2a=4,c=
=1,则2a=4,c= ![]() ,∴a=2,b=
,∴a=2,b= ![]() =1.
=1.
所以点E的轨迹方程为: ![]() +y2=1.
+y2=1.
(II)(1)当直线l与x轴垂直时,直线l的方程为x=1,显然四边形OARB是平行四边形;(2)当直线l与x轴不垂直时,设直线l:y=kx+m,显然k≠0,m≠0,
设A(x1 , y1),B(x2 , y2),M(xM , yM).
联立方程组 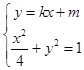 ,得(4k2+1)x2+8kmx+4m2﹣4=0,
,得(4k2+1)x2+8kmx+4m2﹣4=0,
∴x1+x2=﹣ ![]() ,
,
∵ ![]() =
= ![]() ,即M是AB的中点,
,即M是AB的中点,
∴xM= ![]() =﹣
=﹣ ![]() ,yM=kxM+m=
,yM=kxM+m= ![]() ,
,
若四边形OARB是平行四边形,当且仅当AB,OR互相平分,
∴R(﹣ ![]() ,
, ![]() ),
),
代入椭圆方程得: ![]() +
+ ![]() =1,即16k2m2+4m2=16k4+8k2+1,
=1,即16k2m2+4m2=16k4+8k2+1,
又直线l:y=kx+m经过点(1,1),∴m=1﹣k,
∴16k2(1﹣k)2+4(1﹣k)2=16k4+8k2+1,
∴32k3﹣12k2+8k﹣3=0,即(4k2+1)(8k﹣3)=0.
∴k= ![]() ,m=
,m= ![]() ,
,
∴直线l的方程为y= ![]() x+
x+ ![]() 时,四边形OARB是平行四边形,
时,四边形OARB是平行四边形,
综上,直线l的方程为x=1或y= ![]() x+
x+ ![]() .
.
【解析】(I)利用椭圆的定义即可得出E的轨迹方程;(II)讨论直线l的斜率,联立方程组,利用根与系数的关系得出M点坐标,根据平行四边形对角线互相平分得出R点坐标,代入椭圆方程化简即可得出直线l的斜率k.

【题目】对某校高一年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
分组 | 频数 | 频率 |
[10,15) | 10 | 0.25 |
[15,20) | 25 | n |
[20,25) | m | p |
[25,30) | 2 | 0.05 |
合计 | M | 1 |

(1)求出表中M、p及图中a的值;
(2)试估计他们参加社区服务的平均次数;
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至少1人参加社区服务次数在区间[20,25)内的概率.