题目内容
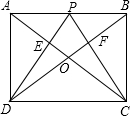 已知如图,矩形ABCD中AB=4cm,BC=3cm,点P是AB上除A,B外任一点,对角线AC,BD相交于点O,DP,CP分别交AC,BD于点E,F且△ADE和BCF的面积之和4cm2,则四边形PEOF的面积为
已知如图,矩形ABCD中AB=4cm,BC=3cm,点P是AB上除A,B外任一点,对角线AC,BD相交于点O,DP,CP分别交AC,BD于点E,F且△ADE和BCF的面积之和4cm2,则四边形PEOF的面积为
- A.1cm2
- B.1.5cm2
- C.2cm2
- D.2.5cm2
A
分析:由已知根据矩形的性质可以求出三角形CPD的面积,那么三角形APD与三角形BCP的面积之和相继求出,再减去△ADE和BCF的面积之和就是三角形AEP与三角形BFP的面积之和,根据矩形的性质能求出三角形AOB的面积,则减去三角形AEP与三角形BFP的面积之和即四边形PEOF的面积.
解答:已知矩形ABCD,
∴△APD的面积+△BPC的面积=矩形ABCD的面积-△CPD的面积=4×3- ×4×3=6,
×4×3=6,
∴△AEP的面积+△BFP的面积=(△APD的面积+△BPC的面积)-△ADE和BCF的面积之和=6-4=2,
已知矩形ABCD,
∴△AOB的面积= ×4×(3×
×4×(3× )=3,
)=3,
∴四边形PEOF的面积=△AOB的面积-(△AEP的面积+△BFP的面积)=3-2=1.
故选A.
点评:此题考查的知识点是矩形的性质及三角形的面积,解题的关键是根据矩形的性质得出三角形APD与三角形BCP的面积之和,然后由已知求出三角形AEP与三角形BFP的面积之和.
分析:由已知根据矩形的性质可以求出三角形CPD的面积,那么三角形APD与三角形BCP的面积之和相继求出,再减去△ADE和BCF的面积之和就是三角形AEP与三角形BFP的面积之和,根据矩形的性质能求出三角形AOB的面积,则减去三角形AEP与三角形BFP的面积之和即四边形PEOF的面积.
解答:已知矩形ABCD,
∴△APD的面积+△BPC的面积=矩形ABCD的面积-△CPD的面积=4×3-
 ×4×3=6,
×4×3=6,∴△AEP的面积+△BFP的面积=(△APD的面积+△BPC的面积)-△ADE和BCF的面积之和=6-4=2,
已知矩形ABCD,
∴△AOB的面积=
 ×4×(3×
×4×(3× )=3,
)=3,∴四边形PEOF的面积=△AOB的面积-(△AEP的面积+△BFP的面积)=3-2=1.
故选A.
点评:此题考查的知识点是矩形的性质及三角形的面积,解题的关键是根据矩形的性质得出三角形APD与三角形BCP的面积之和,然后由已知求出三角形AEP与三角形BFP的面积之和.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
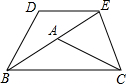 (2012•通州区一模)已知如图,在△ABC中,AB=AC,∠ABC=α,将△ABC以点B为中心,沿逆时针方向旋转α度(0°<α<90°),得到△BDE,点B、A、E恰好在同一条直线上,连接CE.
(2012•通州区一模)已知如图,在△ABC中,AB=AC,∠ABC=α,将△ABC以点B为中心,沿逆时针方向旋转α度(0°<α<90°),得到△BDE,点B、A、E恰好在同一条直线上,连接CE.
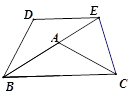
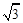 ,请你求出四边形DBCE的面积.
,请你求出四边形DBCE的面积.
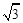 ,请你求出四边形DBCE的面积.
,请你求出四边形DBCE的面积. 已知如图,在△ABC中,AB=AC,∠ABC=α,将△ABC以点B为中心,沿逆时针方向旋转α度(0°<α<90°),得到△BDE,点B、A、E恰好在同一条直线上,连接CE.
已知如图,在△ABC中,AB=AC,∠ABC=α,将△ABC以点B为中心,沿逆时针方向旋转α度(0°<α<90°),得到△BDE,点B、A、E恰好在同一条直线上,连接CE. ,请你求出四边形DBCE的面积.
,请你求出四边形DBCE的面积.