题目内容
在直角坐标系xoy中,将面积为3的直角三角形AGO沿直线y=x翻折,得到三角形CHO,连接AC,已知反比例函数y=| k | x |
(1)k的值是
(2)在直线y=x图象上任取一点D,作AB⊥AD,AC⊥CB,线段OD交AC于点F,交AB于点E,P为直线OD上一动点,连接PB、PC、CE.
㈠如图②,已知点A的横坐标为1,当四边形AECD为正方形时,求三角形PBC的面积;
㈡如图③,若已知四边形PEBC为菱形,求证四边形PBCD是平行四边形;
㈢若D、P两点均在直线y=x上运动,当∠ADC=60°,且三角形PBC的周长最小时,请直接写出三角形PBC与四边形ABCD的面积之比.
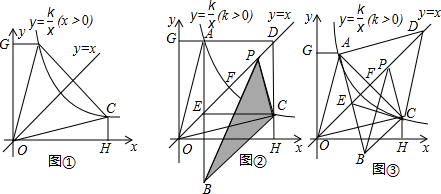
分析:(1)已知△AOG的面积为3,即A点横、纵坐标的乘积为6,由此可得k的值.
(2)①已知了A点横坐标,根据双曲线的解析式可确定A点坐标,根据旋转的性质即可得到点C的坐标;若四边形AECD是正方形,易证得四边形EBCD是平行四边形,即ED、BC间的距离相等,因此△PCB的面积是定值,且是正方形面积的一半,由此得解.
②易知△AGO、△CHO关于直线y=x对称,那么OD垂直平分AC,由于∠AB⊥AD,则必有EC⊥CD,再根据菱形的对角线互相垂直,即可得到所求的结论.
③由于OD垂直平分AC,且D在直线OD上,若∠ADC=60°,那么△ACD是等边三角形,在Rt△EAD中,AF⊥DE,且∠ADE=30°,易证得DF=3EF,即△DAC是△AEC面积的3倍;由于A、C关于直线y=x对称,因此当P、E重合时,△PBC的周长最小,此时E是斜边AB的中点,即AE=BE,由此可证得△BPC、△AEC的面积相等,即:△ACD也是△PBC面积的3倍,由此可求得四边形ABCD和△PBC的面积比.
(2)①已知了A点横坐标,根据双曲线的解析式可确定A点坐标,根据旋转的性质即可得到点C的坐标;若四边形AECD是正方形,易证得四边形EBCD是平行四边形,即ED、BC间的距离相等,因此△PCB的面积是定值,且是正方形面积的一半,由此得解.
②易知△AGO、△CHO关于直线y=x对称,那么OD垂直平分AC,由于∠AB⊥AD,则必有EC⊥CD,再根据菱形的对角线互相垂直,即可得到所求的结论.
③由于OD垂直平分AC,且D在直线OD上,若∠ADC=60°,那么△ACD是等边三角形,在Rt△EAD中,AF⊥DE,且∠ADE=30°,易证得DF=3EF,即△DAC是△AEC面积的3倍;由于A、C关于直线y=x对称,因此当P、E重合时,△PBC的周长最小,此时E是斜边AB的中点,即AE=BE,由此可证得△BPC、△AEC的面积相等,即:△ACD也是△PBC面积的3倍,由此可求得四边形ABCD和△PBC的面积比.
解答:(1)解:设A(a,b),(a>0,b>0);
则AG=a,OG=b,由△AGO的面积是3,即ab=6;
∴k=ab=6.(1分)
(2)解:(一)∵双曲线的解析式为:y=
(x > 0),A为双曲线上的点,且横坐标为1,
可求得A点纵坐标为6;
又∵四边形AECD为正方形,点E在直线y=x上,
∴E(1,1),
∴AECD为正方形边长为5,对角线AC长为5
,AC⊥ED,AE∥CD;
又∵AB⊥AD,
∴ED∥BC,EB∥CD,
∴四边形EBCD为平行四边形,
∴ED=BC,
∵FC⊥BC,
∴S△PBC=
FC • BC=
AC • BC=
AC2,
∵正方形ABCD对角线AC=5
,
∴S△PBC=
=12.5.(4分)
(二)证明:∵四边形PEBC为菱形,
∴EP∥BC;
∵△AGO与△CHO关于y=x对称,
∴OD⊥平分AC;
又∵AB⊥AD,
∴EC⊥CD;
又∵EC⊥PB,
∴PB∥CD;
∴四边形PBCD为平行四边形.(6分)
(三)∵OD垂直平分AC,
∴AD=CD,AE=EC,且F是AC的中点;
在Rt△ABC中,F是AC中点,且EF⊥AC、BC⊥AC,
∴EF是△ABC的中位线,即E是AB的中点,
∴AE=BE;
由于A、C关于直线y=x对称,所以当P、E重合时,△PBC的周长最小;
此时AP=BP,即S△PBC=S△AEC;
△ADC中,由于OD垂直平分AC,若∠ADC=60°,可得:
△ABC是等边三角形,且∠ADE=30°;
在Rt△ADE中,AF⊥DE,∠ADE=30°,易得DF=3EF;
∴S△ADC=3S△AEC=3S△PBC,
故:
=
.(8分)
则AG=a,OG=b,由△AGO的面积是3,即ab=6;
∴k=ab=6.(1分)
(2)解:(一)∵双曲线的解析式为:y=
| 6 |
| x |
可求得A点纵坐标为6;
又∵四边形AECD为正方形,点E在直线y=x上,
∴E(1,1),
∴AECD为正方形边长为5,对角线AC长为5
| 2 |
又∵AB⊥AD,
∴ED∥BC,EB∥CD,
∴四边形EBCD为平行四边形,
∴ED=BC,
∵FC⊥BC,
∴S△PBC=
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
∵正方形ABCD对角线AC=5
| 2 |
∴S△PBC=
| 25 |
| 2 |
(二)证明:∵四边形PEBC为菱形,
∴EP∥BC;
∵△AGO与△CHO关于y=x对称,
∴OD⊥平分AC;
又∵AB⊥AD,
∴EC⊥CD;
又∵EC⊥PB,
∴PB∥CD;
∴四边形PBCD为平行四边形.(6分)
(三)∵OD垂直平分AC,
∴AD=CD,AE=EC,且F是AC的中点;
在Rt△ABC中,F是AC中点,且EF⊥AC、BC⊥AC,
∴EF是△ABC的中位线,即E是AB的中点,
∴AE=BE;
由于A、C关于直线y=x对称,所以当P、E重合时,△PBC的周长最小;
此时AP=BP,即S△PBC=S△AEC;
△ADC中,由于OD垂直平分AC,若∠ADC=60°,可得:
△ABC是等边三角形,且∠ADE=30°;
在Rt△ADE中,AF⊥DE,∠ADE=30°,易得DF=3EF;
∴S△ADC=3S△AEC=3S△PBC,
故:
| S△PBC |
| S四边形ABCD |
| 1 |
| 5 |
点评:此题是反比例函数的综合题,涉及到反比例函数解析式的确定、图形面积的求法、平行四边形及正方形的性质、线段垂直平分线的性质以及轴对称图形的性质等知识,综合性强,难度较大.

练习册系列答案
相关题目

 在直角坐标系xoy中,函数y=4x的图象与反比例函数y=
在直角坐标系xoy中,函数y=4x的图象与反比例函数y= (2012•北京二模)已知:如图,在直角坐标系xOy中,点A(8,0)、B(0,6),点C在x轴的负半轴上,AB=AC.动点M在x轴上从点C向点A移动,动点N在线段AB上从点A向点B移动,点M、N同时出发,且移动的速度都为每秒1个单位,移动时间为t秒(0<t<10).
(2012•北京二模)已知:如图,在直角坐标系xOy中,点A(8,0)、B(0,6),点C在x轴的负半轴上,AB=AC.动点M在x轴上从点C向点A移动,动点N在线段AB上从点A向点B移动,点M、N同时出发,且移动的速度都为每秒1个单位,移动时间为t秒(0<t<10). 析式为y=x2-mx+n.方程x2-mx+n=0的两根倒数和为-4.
析式为y=x2-mx+n.方程x2-mx+n=0的两根倒数和为-4.