题目内容
【题目】定义:如图1,点C在线段AB上,若满足AC2=BCAB,则称点C为线段AB的黄金分割点.
如图2,△ABC中,AB=AC=1,∠A=36°,BD平分∠ABC交AC于点D.
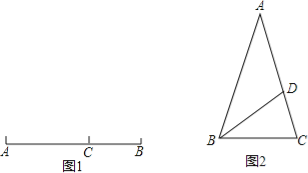
(1)求证:点D是线段AC的黄金分割点;
(2)求出线段AD的长.
【答案】 (1)详见解析
(2) AD=![]()
【解析】
(1)判断△ABC∽△BDC,根据对应边成比例可得出答案。
(2)根据(1)列出方程即可求出AD的长度。
解:(1)∵∠A=36°,AB=AC,∴∠ABC=∠ACB=72°。
∵BD平分∠ABC,∴∠CBD=∠ABD=36°,∠BDC=72°。∴AD=BD,BC=BD。
∴△ABC∽△BDC。∴![]() ,即
,即![]() 。∴AD2=ACCD。
。∴AD2=ACCD。
∴点D是线段AC的黄金分割点。
(2)由(1)AD2=ACCD,即AD2=AC(AC﹣AD),AD2=1﹣AD,AD2+AD﹣1=。
解得AD=![]() (舍去负值)。
(舍去负值)。
∴AD=![]() 。
。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目