题目内容
【题目】如图①有一个宝塔,它的地基边缘是周长为26m的正五边形ABCDE(如图②),点O为中心.(下列各题结果精确到0.1m)
(1)求地基的中心到边缘的距离;
(2)己知塔的墙体宽为1m,现要在塔的底层中心建一圆形底座的塑像,并且留出最窄处为1.6m的观光通道,问塑像底座的半径最大是多少?
【答案】
(1)
解:作OM⊥AB于点M,连接OA、OB,则OM为边心距,∠AOB是中心角.
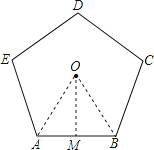
由正五边形性质得∠AOB=360°÷5=72°.
又AB= ![]() ×26=5.2,
×26=5.2,
∴AM=2.6,∠AOM=36°,
在Rt△AMO中,边心距OM= ![]()
(2)
3.6-1-1.6=1(m).
答:地基的中心到边缘的距离约为3.6m,塑像底座的半径最大约为1m.
【解析】(1)构造一个由正多边形的边心距、半边和半径组成的直角三角形.根据正五边形的性质得到半边所对的角是36°,再根据题意中的周长求得该正五边形的半边是26÷10=2.6,最后由该角的正切值进行求解;(2)根据(1)中的结论、塔的墙体宽为1m和最窄处为1.6m的观光通道,进行计算.
【考点精析】解答此题的关键在于理解正多边形和圆的相关知识,掌握圆的内接四边形的对角互补,并且任何一个外角都等于它的内对角;圆的外切四边形的两组对边的和相等.

练习册系列答案
相关题目