题目内容
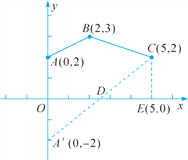
【题目】如图,某公路(可视为x轴)的同一侧有A,B,C三个村庄,要在公路边建一货仓D,向A,B,C三个村庄送农用物资,路线是D→A→B→C→D.
(1)试问:在公路边是否存在一点D,使送货路程最短?
(2)求出点D的坐标,并说明理由.
【答案】(1)存在(2)(![]() ,0)
,0)
【解析】试题分析:本题考查最短路线问题,因为路程即为DA+AB+BC+DC,AB+BC的长度固定,所以要使路程最短,只需DA+DC最短即可,根据小马饮水问题的解决方法可知,作点A关于x轴对称的点A′,然后连接A′C, A′C与x轴的交点即为点D, A′C即为DA+DC最短距离,根据待定系数法求A′C的直线解析式,再求直线与x轴的交点.
(1)存在.
(2)∵路程即为DA+AB+BC+DC,AB+BC的长度固定,∴要使路程最短,只需DA+DC最短即可.
作点A关于x轴的对称点A′(0,-2),连结A′C,则A′C与x轴的交点即为点D.
过点C作CE⊥x轴于点E,则点E(5,0),易得△OA′D≌△ECD,得OD=ED,∴点D![]() .
.

练习册系列答案
相关题目