题目内容
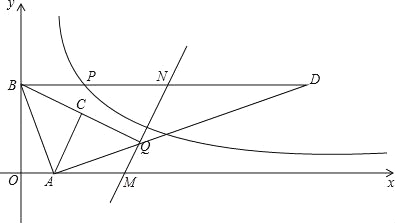
【题目】如图所示,A,B是坐标轴正半轴上的两点,过点B作PB⊥y轴交双曲线y=![]() (x>0)于P点,A,B两点的坐标分别为(1,0),(0,3),x轴上的动点M在点A的右侧,动点N在射线BP上,过点A作AB的垂线,交射线BP于D点,交直线MN于Q点,连结BQ,取BQ的中点C,若以A,C,N,Q为顶点的四边形是平行四边形,则Q点的坐标为 .
(x>0)于P点,A,B两点的坐标分别为(1,0),(0,3),x轴上的动点M在点A的右侧,动点N在射线BP上,过点A作AB的垂线,交射线BP于D点,交直线MN于Q点,连结BQ,取BQ的中点C,若以A,C,N,Q为顶点的四边形是平行四边形,则Q点的坐标为 .
【答案】(4,1)或(28,9).
【解析】
试题分析:∵A(1,0),B(0,3),
∴直线AB的解析式为y=﹣3x+3,
∵AD⊥AB,
∴直线AD的解析式为y=![]() x﹣
x﹣![]() ,
,
∵BD⊥y轴,
∴BD∥OA,
∴D(10,3),
①如图1中,当Q在线段AD上时,作QE⊥x轴于E,DF⊥x轴于F.
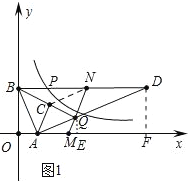
∵四边形ACNQ是平行四边形,
∴AQ=CN,CN∥AD,
∵BC=CQ,
∴BN=ND,
∴DQ=2CN=2AQ,
∵QE∥DF,
∴![]() ,
,
∵AF=9,DF=3,
∴QE=1,AE=3,
∴点Q坐标为(4,1).
②如图2中,当点Q在AD的延长线上时,作QF⊥x轴于F,DE⊥AF于E.
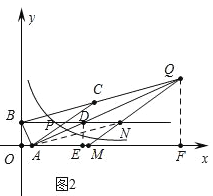
∵四边形ACQN是平行四边形,
∴AN∥BQ,AN=CQ,
∴![]() ,∵BC=CQ,
,∵BC=CQ,
∴![]() ,
,
∵DE∥QF,
∴![]() ,
,
∵AE=9,DE=3,
∴QF=9,AF=27,
∴点Q坐标(28,9),
综上所述点Q坐标(4,1)或(28,9).

练习册系列答案
相关题目