题目内容
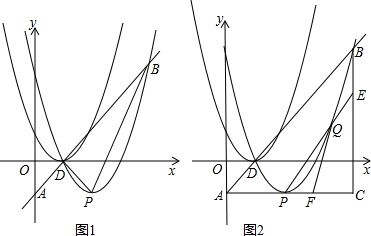
17、如图，抛物线C1：y=x2-4x的对称轴为直线x=a，将抛物线C1向上平移5个单位长度得到抛物线C2，则抛物线C2的顶点坐标为
（2，1）
；图中的两条抛物线、直线x=a与y轴所围成的图形（图中阴影部分）的面积为
10
．分析：先求出C1的顶点坐标，再根据平移的性质求出C1的顶点坐标，E的坐标，可见红色部分面积等于黄色部分的面积，即求出平行四边形OGFE的面积即可．
解答：
解：在抛物线C1：y=x2-4x中，
C1的顶点G的坐标为（2，-4），
由于抛物线C1向上平移5个单位长度得到抛物线C2，
故F点坐标为（2，1），
E点坐标为（0，5）．
故平行四边形OGFE的面积为5×2=10．
故答案为：（2，1）；10．
解：在抛物线C1：y=x2-4x中，C1的顶点G的坐标为（2，-4），
由于抛物线C1向上平移5个单位长度得到抛物线C2，
故F点坐标为（2，1），
E点坐标为（0，5）．
故平行四边形OGFE的面积为5×2=10．
故答案为：（2，1）；10．
点评：此题考查了平移的性质，根据抛物线的图象上点的坐标特征，确定平行四边形的EOGF的面积是解题的关键．
练习册系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
16、如图，抛物线C1：y=x2-4x的对称轴为直线x=a，将抛物线C1向上平移5个单位长度得到抛物线C2，则图中的两条抛物线、直线x=a与y轴所围成的图形（图中阴影部分）的面积为
26、已知：如图，抛物线C1，C2关于x轴对称；抛物线C1，C3关于y轴对称．抛物线C1，C2，C3与x轴相交于A、B、C、D四点；与y相交于E、F两点；H、G、M分别为抛物线C1，C2，C3的顶点．HN垂直于x轴，垂足为N，且|OE|＞|HN|，|AB|≠|HG|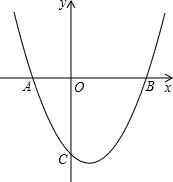
如图，抛物线c1：y=ax2-2ax-c与x轴交于A、B，且AB=6，与y轴交于C（0，-4 ）．
