题目内容
如图，抛物线C1：y=ax2+bx+1的顶点坐标为D（1，0），（1）求抛物线C1的解析式；
（2）如图1，将抛物线C1向右平移1个单位，向下平移1个单位得到抛物线C2，直线y=x+c，经过点D交y轴于点A，交抛物线C2于点B，抛物线C2的顶点为P，求△DBP的面积
（3）如图2，连接AP，过点B作BC⊥AP于C，设点Q为抛物线上点P至点B之间的一动点，连接PQ并延长交BC于点E，连接BQ并延长交AC于点F，试证明：FC（AC+EC）为定值．
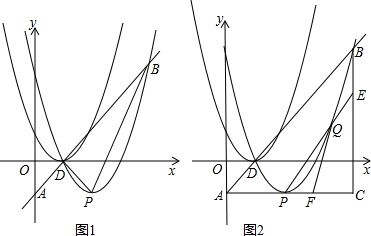
分析：（1）已知顶点P的坐标，设抛物线的顶点式为：y=a（x-1）2，将点（0，1）代入即可；
（2）根据平移规律求出平移后抛物线的顶点坐标，即P（2，-1），根据顶点式，得平移后抛物线解析式y=（x-2）2-1，由解析式，得A（0，-1），B（4，3），可求△DBP的面积；
（3）由QM∥CE，得△PQM∽△PEC，利用相似比求EC，由QN∥FC，得△BQN∽△BFC，利用相似比求FC，已知AC=4，再计算FC（AC+EC）为定值．
（2）根据平移规律求出平移后抛物线的顶点坐标，即P（2，-1），根据顶点式，得平移后抛物线解析式y=（x-2）2-1，由解析式，得A（0，-1），B（4，3），可求△DBP的面积；
（3）由QM∥CE，得△PQM∽△PEC，利用相似比求EC，由QN∥FC，得△BQN∽△BFC，利用相似比求FC，已知AC=4，再计算FC（AC+EC）为定值．
解答：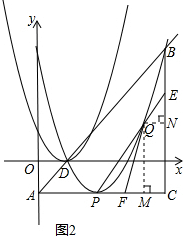
（1）解：∵抛物线顶点为D（1，0），经过点（0，1）
∴可设抛物线的解析式为：y=a（x-1）2，将点（0，1）代入，得a=1，
∴抛物线的解析式为y=x2-2x+1；
（2）解：根据题意，平移后顶点坐标P（2，-1）
∴抛物线的解析式为：y=（x-2）2-1，
∴A（0，-1），B（4，3），
∴S△DBP=3；
（3）证明：过点Q作QM⊥AC于点M，过点Q作QN⊥BC于点N，
设点Q的坐标是（t，t2-4t+3），则QM=CN=（t-2）2，MC=QN=4-t．
∵QM∥CE，
∴△PQM∽△PEC，
∴
=
，
即
=
，
得EC=2（t-2），
∵QN∥FC，
∴△BQN∽△BFC，
∴
=
，
即
=
，
得FC=
，
又∵AC=4，
∴FC（AC+EC）=
[4+2（t-2）]=8，
即FC（AC+EC）为定值8．
（1）解：∵抛物线顶点为D（1，0），经过点（0，1）∴可设抛物线的解析式为：y=a（x-1）2，将点（0，1）代入，得a=1，
∴抛物线的解析式为y=x2-2x+1；
（2）解：根据题意，平移后顶点坐标P（2，-1）
∴抛物线的解析式为：y=（x-2）2-1，
∴A（0，-1），B（4，3），
∴S△DBP=3；
（3）证明：过点Q作QM⊥AC于点M，过点Q作QN⊥BC于点N，
设点Q的坐标是（t，t2-4t+3），则QM=CN=（t-2）2，MC=QN=4-t．
∵QM∥CE，
∴△PQM∽△PEC，
∴
| QM |
| EC |
| PM |
| PC |
即
| (t-2)2 |
| EC |
| t-2 |
| 2 |
得EC=2（t-2），
∵QN∥FC，
∴△BQN∽△BFC，
∴
| QN |
| FC |
| BN |
| BC |
即
| 4-t |
| FC |
| 3-(t2-4t+3) |
| 4 |
得FC=
| 4 |
| t |
又∵AC=4，
∴FC（AC+EC）=
| 4 |
| t |
即FC（AC+EC）为定值8．
点评：本题考查了二次函数的解析式的求法，相似三角形的判定与性质的综合能力培养．要会利用数形结合的思想把代数和几何图形结合起来，利用点的坐标的意义表示线段的长度，从而求出线段之间的关系．
练习册系列答案
相关题目
16、如图，抛物线C1：y=x2-4x的对称轴为直线x=a，将抛物线C1向上平移5个单位长度得到抛物线C2，则图中的两条抛物线、直线x=a与y轴所围成的图形（图中阴影部分）的面积为
26、已知：如图，抛物线C1，C2关于x轴对称；抛物线C1，C3关于y轴对称．抛物线C1，C2，C3与x轴相交于A、B、C、D四点；与y相交于E、F两点；H、G、M分别为抛物线C1，C2，C3的顶点．HN垂直于x轴，垂足为N，且|OE|＞|HN|，|AB|≠|HG|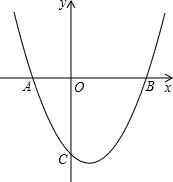
如图，抛物线c1：y=ax2-2ax-c与x轴交于A、B，且AB=6，与y轴交于C（0，-4 ）．