��Ŀ����
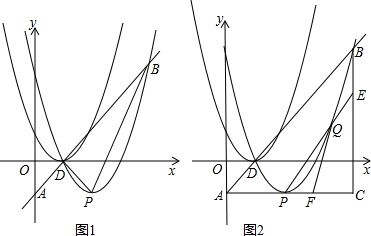
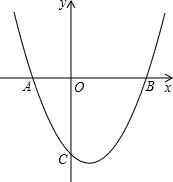 ��ͼ��������c1��y=ax2-2ax-c��x�ύ��A��B����AB=6����y�ύ��C��0��-4 ����
��ͼ��������c1��y=ax2-2ax-c��x�ύ��A��B����AB=6����y�ύ��C��0��-4 ������1����������c1�Ľ���ʽ��
��2����������c1���Ƿ����P��Q����P�ڵ�Q���Ϸ������㣬ʹ����A��C��P��QΪ������ı���Ϊֱ�����Σ������ڣ���P��Q�������ꣻ�������ڣ���˵�����ɣ�
��3��������c2��������c1����x��Գƣ�ֱ��x=m�ֱ�c1��c2��D��E���㣬ֱ��x=n�ֱ�c1��c2��M��N���㣬���ı���DMNEΪƽ���ı��Σ����ж�m��n���������ϵ����˵�����ɣ�
��������1����C��0��-4�����������ߵĽ���ʽ���c=4���õ�y=ax2-2ax-4������AB=6�����������ʽ�������a��ֵ�����뼴�ɣ�
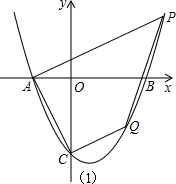
��2��������������ٵ���PAC=��ACQ=90��ʱ������AQ����Q��x��
x2-x-4�����ɹ��ɶ����ó�AQ2=AC2+CQ2���������x��ֵ�����
x2-x-4=-
���õ�Q�����꣬ͬ������P�����ꣻ�ڵ���ACQ=��PQC=90��ʱ����ٽⷨ���ƿ����Q�������P�����꣬���ɵó��𰸣�
��3��m��n���������ϵ��m+n=0����m��0��n��0������������c2��������c1����x��Գƣ��ó��������ߵ���״��ͬ�����ڷ����෴���Ҷ�����x��Գƣ�����ƽ���ı��ε���״�õ�DE��MN��ED=MN��DE�� MN����ֱ��x=1�Գƣ����ɵõ��𰸣�
��2��������������ٵ���PAC=��ACQ=90��ʱ������AQ����Q��x��
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
��3��m��n���������ϵ��m+n=0����m��0��n��0������������c2��������c1����x��Գƣ��ó��������ߵ���״��ͬ�����ڷ����෴���Ҷ�����x��Գƣ�����ƽ���ı��ε���״�õ�DE��MN��ED=MN��DE�� MN����ֱ��x=1�Գƣ����ɵõ��𰸣�
�����1���⣺��C��0��-4�����������ߵĽ���ʽ�ã�c=4��
��y=ax2-2ax-4��
��AB=6��
��|
-
|=6��
��ã�a=0����ȥ����a=
��
��y=
x2-x-4��
��������c1�Ľ���ʽ��y=
x2-x-4��
��2���⣺�ߵ�y=
x2-x-4=0��x=4��-2��
��OA=2��OB=4��
������������ٵ���PAC=��ACQ=90��ʱ��ͼ��1��������AQ����Q��x��
x2-x-4����
�ɹ��ɶ����ã�AQ2=AC2+CQ2��
������x+2��2+(
x2-x-4) 2=22+42+x2+(
x2-x-4+4) 2��
��ã�x=0����ȥ����x=3��
��x=3 ʱ��
x2-x-4=-
��
��Q��3��
����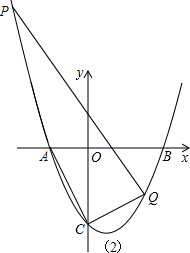
ͬ������P�������ǣ�5��
����
�ڵ���ACQ=��PQC=90��ʱ��ͼ��2������ٽⷨ���ƿ����Q�������ǣ�3��-
����P�������ǣ�-5��
����
�𣺴��ڣ�P��Q������ֱ�Ϊ��5��
������3��-
����-5��
������3��-
����
��3����m��n���������ϵ��m+n=0����m��0��n��0��
�����ǣ���������c2��������c1����x��Գƣ�
���������ߵ���״��ͬ�����ڷ����෴���Ҷ�����x��Գƣ�
��ֱ��x=m�ֱ�c1��c2��D��E���㣬ֱ��x=n�ֱ�c1��c2��M��N���㣬�ı���DMNEΪƽ���ı��Σ�
��ֱ��m n��ֱ��x�ᣨm��n����DE=MN��DE�� MN����ֱ��x=1�Գƣ�
��m+n=2��m��0��n��0��
��y=ax2-2ax-4��
��AB=6��
��|
2a+
| ||
| 2a |
2a-
| ||
| 2a |
��ã�a=0����ȥ����a=
| 1 |
| 2 |
��y=
| 1 |
| 2 |
��������c1�Ľ���ʽ��y=
| 1 |
| 2 |

��2���⣺�ߵ�y=
| 1 |
| 2 |
��OA=2��OB=4��
������������ٵ���PAC=��ACQ=90��ʱ��ͼ��1��������AQ����Q��x��
| 1 |
| 2 |
�ɹ��ɶ����ã�AQ2=AC2+CQ2��
������x+2��2+(
| 1 |
| 2 |
| 1 |
| 2 |
��ã�x=0����ȥ����x=3��
��x=3 ʱ��
| 1 |
| 2 |
| 5 |
| 2 |
��Q��3��
| 5 |
| 2 |

ͬ������P�������ǣ�5��
| 7 |
| 2 |
�ڵ���ACQ=��PQC=90��ʱ��ͼ��2������ٽⷨ���ƿ����Q�������ǣ�3��-
| 5 |
| 2 |
| 27 |
| 2 |
�𣺴��ڣ�P��Q������ֱ�Ϊ��5��
| 7 |
| 2 |
| 5 |
| 2 |
| 27 |
| 2 |
| 5 |
| 2 |
��3����m��n���������ϵ��m+n=0����m��0��n��0��
�����ǣ���������c2��������c1����x��Գƣ�
���������ߵ���״��ͬ�����ڷ����෴���Ҷ�����x��Գƣ�
��ֱ��x=m�ֱ�c1��c2��D��E���㣬ֱ��x=n�ֱ�c1��c2��M��N���㣬�ı���DMNEΪƽ���ı��Σ�
��ֱ��m n��ֱ��x�ᣨm��n����DE=MN��DE�� MN����ֱ��x=1�Գƣ�
��m+n=2��m��0��n��0��
������������Ҫ�����ƽ���ı��ε����ʣ�������ͼ�α任-�Գƣ����ɶ�������һԪ���η���-��ʽ����ֱ�����ε�֪ʶ�����������գ��ۺ�������Щ���ʽ��������ǽ����Ĺؼ�����Ŀ�Ƚϵ��ͣ��Ѷ����У�

��ϰ��ϵ�д�
 ���Ͱ�ͨ�������Сѧ��ʱͬ�����ϵ�д�
���Ͱ�ͨ�������Сѧ��ʱͬ�����ϵ�д� ���Ͱ�ͨ������ϵ�д�
���Ͱ�ͨ������ϵ�д� �ٷ�ѧ����ҵ��������ϵ�д�
�ٷ�ѧ����ҵ��������ϵ�д�
�����Ŀ
 16����ͼ��������C1��y=x2-4x�ĶԳ���Ϊֱ��x=a����������C1����ƽ��5����λ���ȵõ�������C2����ͼ�е����������ߡ�ֱ��x=a��y����Χ�ɵ�ͼ�Σ�ͼ����Ӱ���֣������Ϊ
16����ͼ��������C1��y=x2-4x�ĶԳ���Ϊֱ��x=a����������C1����ƽ��5����λ���ȵõ�������C2����ͼ�е����������ߡ�ֱ��x=a��y����Χ�ɵ�ͼ�Σ�ͼ����Ӱ���֣������Ϊ 26����֪����ͼ��������C1��C2����x��Գƣ�������C1��C3����y��Գƣ�������C1��C2��C3��x���ཻ��A��B��C��D�ĵ㣻��y�ཻ��E��F���㣻H��G��M�ֱ�Ϊ������C1��C2��C3�Ķ��㣮HN��ֱ��x�ᣬ����ΪN����|OE|��|HN|��|AB|��|HG|
26����֪����ͼ��������C1��C2����x��Գƣ�������C1��C3����y��Գƣ�������C1��C2��C3��x���ཻ��A��B��C��D�ĵ㣻��y�ཻ��E��F���㣻H��G��M�ֱ�Ϊ������C1��C2��C3�Ķ��㣮HN��ֱ��x�ᣬ����ΪN����|OE|��|HN|��|AB|��|HG|