Question

在直角坐标平面内，O为原点，点A的坐标为（1，0），点C的坐标为（0，4），直线CM∥x轴（如图所示），点B与点A关于原点对称，直线y=x+b（b为常数）经过点B，且与直线CM相交点D，连接OD，设P在x轴的正半轴上，若△POD为等腰三角形，则点P的坐标为

（5，0）；（6，0）；（

25

6

，0）

．

Answer 1

分析：如图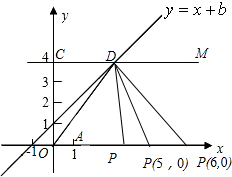
对称点到对称中心的距离相等可求出对称点；待定系数法求y=x+b解析式，把（-1，0）代入y=x+b（b为常数）；二元一次方程组的解是直线的交点，求交点坐标，

y=x+1 y=4

；两边相等的三角形是等腰三角形可确定△POD；分类讨论当OD=OP=5时，P点坐标是（5，0）；当OD=PD=5时，P点坐标是（6，0）；当OP=PD=

25

6

时，P点坐标是（

25

6

，0）．

解答：解：∵点A的坐标为（1，0），点B与点A关于原点对称
∴B点坐标（-1，0）；
∵直线y=x+b（b为常数）经过点B（-1，0），
∴直线y=x+b（b为常数）的解析式 y=x+1
∵点C的坐标为（0，4），直线CM∥x轴（如图所示），
∴直线CM为y=4
∵直线y=x+1（b为常数）经过点B，且与直线CM：y=4  相交点D，
∴D点坐标是（3，4）；
当OD=OP=5时，P点坐标是（5，0）；当OD=PD=5时，P点坐标是（6，0）；当OP=PD=

25

6

时，P点坐标是（

25

6

，0）
综上所述，P点坐标是（5，0）；（6，0）；（

25

6

，0）．
故答案为：（5，0）；（6，0）；（

25

6

，0）．

点评：本题考查了一次函数与二元一次方程组的关系，等腰三角形．要注意△POD为等腰三角形，点P的坐标有三个．