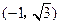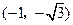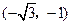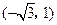题目内容
在直角坐标平面内的机器人接受指令“[a,A]”(a≥0,0°<A<180°)后的行动结果为:在原地顺时针旋转A后,再向正前方沿直线行走a个单位长度.若机器人的位置在原点,正前方为y轴的负半轴,则它完成一次指令[2,60°]后位置的坐标为( )
A、(-1,
| ||
B、(-1,-
| ||
C、(-
| ||
D、(-
|
分析:根据题意画出图形,得出OA=2,∠AOC=60°,求出∠AOB,根据直角三角形的性质和勾股定理求出OB、AB即可.
解答: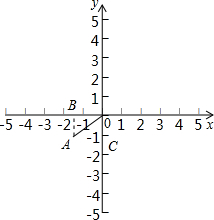 解:由已知得到:OA=2,∠COA=60°,
解:由已知得到:OA=2,∠COA=60°,
过A作AB⊥X轴于B,
∴∠BOA=90°-60°=30°,
∴AB=1,
由勾股定理得:OB=
,
∴A的坐标是(-
,-1).
故选C.
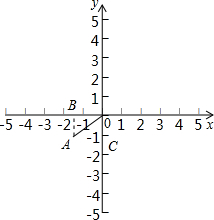 解:由已知得到:OA=2,∠COA=60°,
解:由已知得到:OA=2,∠COA=60°,过A作AB⊥X轴于B,
∴∠BOA=90°-60°=30°,
∴AB=1,
由勾股定理得:OB=
| 3 |
∴A的坐标是(-
| 3 |
故选C.
点评:本题主要考查对勾股定理,含30度直角三角形的性质,坐标与图形变化-旋转等知识点的理解和掌握,能正确画出图形是解此题的关键.

练习册系列答案
相关题目
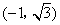 B、
B、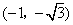 C、
C、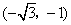 D、
D、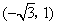
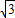 )
)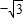 )
)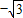 ,-1)
,-1)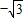 ,1)
,1)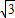 )
)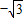 )
)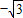 ,-1)
,-1)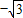 ,1)
,1)