Question

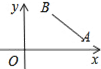
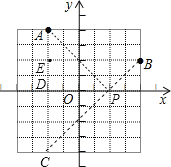
【题目】如图，在平面直角坐标系中，点A（﹣2，4），B（4，2），在x轴上取一点P，使点P到点A和点B的距离之和最小，则点P的坐标是（ ）

A.（﹣2，0） B.（4，0） C.（2，0） D.（0，0）

Answer 1

【答案】C

【解析】

试题分析：作A关于x轴的对称点C，连接AC交x轴于D，连接BC交交x轴于P，连接AP，此时点P到点A和点B的距离之和最小，求出C（的坐标，设直线CB的解析式是y=kx+b，把C、B的坐标代入求出解析式是y=x﹣2，把y=0代入求出x即可．

解：作A关于x轴的对称点C，连接AC交x轴于D，连接BC交交x轴于P，连接AP，

则此时AP+PB最小，

即此时点P到点A和点B的距离之和最小，

∵A（﹣2，4），

∴C（﹣2，﹣4），

设直线CB的解析式是y=kx+b，

把C、B的坐标代入得：，

解得：k=1，b=﹣2，

∴y=x﹣2，

把y=0代入得：0=x﹣2，

x=2，

即P的坐标是（2，0），

故选C．