题目内容
【题目】已知：如图，在∠POQ内部有两点M、N，∠MOP＝∠NOQ.
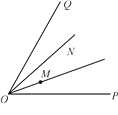
(1)画图并简要说明画法：在射线OP上取一点A，使点A到点M和点N的距离和最小；在射线OQ上取一点B，使点B到点M和点N的距离和最小；
(2)直接写出AM＋AN与BM＋BN的大小关系．
【答案】(1)见解析;(2)AM＋AN＝BM＋BN.
【解析】试题分析：
(1)根据轴对称的性质，分别作点M，N关于OP，OQ的对称点M′，N′，连接MM′，NN′交OP，OQ于点A，B.
（2）由轴对称的性质可知AM+AN=M′N，BM+BN=MN′，
试题解析：
(1)图略，点A，B即为所求．画法：①作点M关于射线OP的对称点M′；②连接M′N交OP于点A；③作点N关于射线OQ的对称点N′；④连接N′M交OQ于点B.
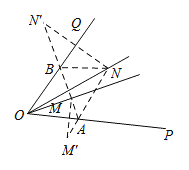
(2)AM＋AN＝BM＋BN.
练习册系列答案
相关题目
