题目内容
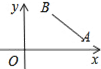
【题目】如图,在直角坐标系中有线段AB,AB=50cm,A、B到x轴的距离分别为10cm和40cm,B点到y轴的距离为30cm,现在在x轴、y轴上分别有动点P、Q,当四边形PABQ的周长最短时,则这个值为( )
A. 50 B. 50![]() C. 50
C. 50![]() -50 D. 50
-50 D. 50![]() +50
+50
【答案】D
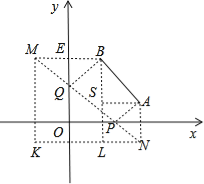
【解析】试题分析:过B点作BM⊥y轴交y轴于E点,截取EM=BE,过A点作AN⊥x轴交x轴于F点,截取NF=AF,连接MN交X,Y轴分别为P,Q点,此时四边形PABQ的周长最短,根据题目所给的条件可求出周长.
解:过B点作BM⊥y轴交y轴于E点,截取EM=BE,过A点作AN⊥x轴交x轴于F点,截取NF=AF,连接MN交x,y轴分别为P,Q点,
过M点作MK⊥x轴,过N点作NK⊥y轴,两线交于K点.
MK=40+10=50,
作BL⊥x轴交KN于L点,过A点作AS⊥BP交BP于S点.
∵LN=AS=![]() =40.
=40.
∴KN=60+40=100.
∴MN=![]() =50
=50![]() .
.
∵MN=MQ+QP+PN=BQ+QP+AP=50![]() .
.
∴四边形PABQ的周长=50![]() +50.
+50.
故选D.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目