题目内容
 (2012•山西)综合与实践:如图,在平面直角坐标系中,抛物线y=-x2+2x+3与x轴交于A、B两点,与y轴交于点C,点D是该抛物线的顶点.
(2012•山西)综合与实践:如图,在平面直角坐标系中,抛物线y=-x2+2x+3与x轴交于A、B两点,与y轴交于点C,点D是该抛物线的顶点.(1)求直线AC的解析式及B、D两点的坐标;
(2)点P是x轴上一个动点,过P作直线l∥AC交抛物线于点Q,试探究:随着P点的运动,在抛物线上是否存在点Q,使以点A、P、Q、C为顶点的四边形是平行四边形?若存在,请直接写出符合条件的点Q的坐标;若不存在,请说明理由.
(3)请在直线AC上找一点M,使△BDM的周长最小,求出M点的坐标.
分析:(1)根据抛物线的解析式可得出A、B、C、D的坐标,设AC解析式为y=k1x+b1(k1≠0),利用待定系数法求解即可.
(2)先根据题意结合图形,画出点P和点Q的位置,然后利用平行线的性质,及抛物线上点的坐标特点可求出三个Q的坐标.
(3)因为BD的长固定,要使△BDM的周长最小,只需满足BM+DM的值最小即可,作点B关于AC的对称点B',连接B'D,则与AC交点即是点M的位置,然后利用相似三角形的性质求出B'的坐标,得出B'D的解析式,继而联立AC与B'D的解析式可得出点M的坐标.
(2)先根据题意结合图形,画出点P和点Q的位置,然后利用平行线的性质,及抛物线上点的坐标特点可求出三个Q的坐标.
(3)因为BD的长固定,要使△BDM的周长最小,只需满足BM+DM的值最小即可,作点B关于AC的对称点B',连接B'D,则与AC交点即是点M的位置,然后利用相似三角形的性质求出B'的坐标,得出B'D的解析式,继而联立AC与B'D的解析式可得出点M的坐标.
解答:解:(1)当y=0时,-x2+2x+3=0,解得x1=-1,x2=3.
∵点A在点B的左侧,
∴A、B的坐标分别为(-1,0),(3,0).
当x=0时,y=3.
∴C点的坐标为(0,3)
设直线AC的解析式为y=k1x+b1(k1≠0),
则
,
解得
,
∴直线AC的解析式为y=3x+3.
∵y=-x2+2x+3=-(x-1)2+4,
∴顶点D的坐标为(1,4).
(2)抛物线上有三个这样的点Q,
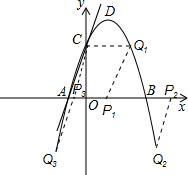
①当点Q在Q1位置时,Q1的纵坐标为3,代入抛物线可得点Q1的坐标为(2,3);
②当点Q在点Q2位置时,点Q2的纵坐标为-3,代入抛物线可得点Q2坐标为(1+
,-3);
③当点Q在Q3位置时,点Q3的纵坐标为-3,代入抛物线解析式可得,点Q3的坐标为(1-
,-3);
综上可得满足题意的点Q有三个,分别为:Q1(2,3),Q2(1+
,-3),Q3(1-
,-3).
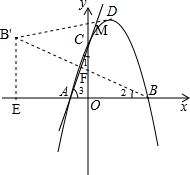
(3)过点B作BB′⊥AC于点F,使B′F=BF,则B′为点B关于直线AC 的对称点.连接B′D交直线AC于点M,则点M为所求,
过点B′作B′E⊥x轴于点E.
∵∠1和∠2都是∠3的余角,
∴∠1=∠2.
∴Rt△AOC∽Rt△AFB,
∴
=
,
由A(-1,0),B(3,0),C(0,3)得OA=1,OB=3,OC=3,
∴AC=
,AB=4.
∴
=
,
∴BF=
,
∴BB′=2BF=
,
由∠1=∠2可得Rt△AOC∽Rt△B′EB,
∴
=
=
,
∴
=
=
,即
=
=
.
∴B′E=
,BE=
,
∴OE=BE-OB=
-3=
.
∴B′点的坐标为(-
,
).
设直线B′D的解析式为y=k2x+b2(k2≠0).
∴
,
解得
,
∴直线B'D的解析式为:y=
x+
,
联立B'D与AC的直线解析式可得:
,
解得
,
∴M点的坐标为(
,
).
∵点A在点B的左侧,
∴A、B的坐标分别为(-1,0),(3,0).
当x=0时,y=3.
∴C点的坐标为(0,3)
设直线AC的解析式为y=k1x+b1(k1≠0),
则
|
解得
|
∴直线AC的解析式为y=3x+3.
∵y=-x2+2x+3=-(x-1)2+4,
∴顶点D的坐标为(1,4).
(2)抛物线上有三个这样的点Q,

①当点Q在Q1位置时,Q1的纵坐标为3,代入抛物线可得点Q1的坐标为(2,3);
②当点Q在点Q2位置时,点Q2的纵坐标为-3,代入抛物线可得点Q2坐标为(1+
| 7 |
③当点Q在Q3位置时,点Q3的纵坐标为-3,代入抛物线解析式可得,点Q3的坐标为(1-
| 7 |
综上可得满足题意的点Q有三个,分别为:Q1(2,3),Q2(1+
| 7 |
| 7 |

(3)过点B作BB′⊥AC于点F,使B′F=BF,则B′为点B关于直线AC 的对称点.连接B′D交直线AC于点M,则点M为所求,
过点B′作B′E⊥x轴于点E.
∵∠1和∠2都是∠3的余角,
∴∠1=∠2.
∴Rt△AOC∽Rt△AFB,
∴
| CO |
| BF |
| CA |
| AB |
由A(-1,0),B(3,0),C(0,3)得OA=1,OB=3,OC=3,
∴AC=
| 10 |
∴
| 3 |
| BF |
| ||
| 4 |
∴BF=
| 12 | ||
|
∴BB′=2BF=
| 24 | ||
|
由∠1=∠2可得Rt△AOC∽Rt△B′EB,
∴
| AO |
| B′E |
| CO |
| BE |
| CA |
| BB′ |
∴
| 1 |
| B′E |
| 3 |
| BE |
| ||||
|
| 1 |
| B′E |
| 3 |
| BE |
| 5 |
| 12 |
∴B′E=
| 12 |
| 5 |
| 36 |
| 5 |
∴OE=BE-OB=
| 36 |
| 5 |
| 21 |
| 5 |
∴B′点的坐标为(-
| 21 |
| 5 |
| 12 |
| 5 |
设直线B′D的解析式为y=k2x+b2(k2≠0).
∴
|
解得
|
∴直线B'D的解析式为:y=
| 4 |
| 13 |
| 48 |
| 13 |
联立B'D与AC的直线解析式可得:
|
解得
|
∴M点的坐标为(
| 9 |
| 35 |
| 132 |
| 35 |
点评:此题考查了二次函数的综合应用,涉及了相似三角形的判定与性质、平行四边形的性质,解答本题需要我们熟练各个知识点的内容,认真探究题目,谨慎作答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2012•山西)如图,在平面直角坐标系中,矩形OABC的对角线AC平行于x轴,边OA与x轴正半轴的夹角为30°,OC=2,则点B的坐标是
(2012•山西)如图,在平面直角坐标系中,矩形OABC的对角线AC平行于x轴,边OA与x轴正半轴的夹角为30°,OC=2,则点B的坐标是