题目内容
如图,抛物线y1=a(x+2)2-3与 交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B、C,则以下结论:①无论x取何值,y2总是正数;②a=1;③当x=0时,y2-y1=4;④2AB=3AC.其中正确的是( )
交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B、C,则以下结论:①无论x取何值,y2总是正数;②a=1;③当x=0时,y2-y1=4;④2AB=3AC.其中正确的是( )
A.①② B.②③ C.③④ D.①④
D.
解析试题分析:①∵抛物线y2=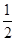 (x-3)2+1开口向上,顶点坐标在x轴的上方,
(x-3)2+1开口向上,顶点坐标在x轴的上方,
∴无论x取何值,y2的值总是正数,故本小题正确;
②把A(1,3)代入,抛物线y1=a(x+2)2-3得,3=a(1+2)2-3,解得a=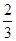 ,故本小题错误;
,故本小题错误;
③由两函数图象可知,抛物线y1=a(x+2)2-3解析式为y1=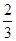 (x+2)2-3,
(x+2)2-3,
当x=0时,y1=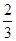 (0+2)2-3=-
(0+2)2-3=-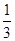 ,y2=
,y2=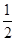 (0-3)2+1=
(0-3)2+1=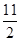 ,故y2-y1=-
,故y2-y1=-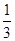 -
-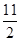 =-
=-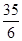 ,故本小题错误;
,故本小题错误;
④∵物线y1=a(x+2)2-3与y2=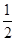 (x-3)2+1交于点A(1,3),
(x-3)2+1交于点A(1,3),
∴y1的对称轴为x=-2,y2的对称轴为x=3,
∴B(-5,3),C(5,3)
∴AB=6,AC=4,
∴2AB=3AC,故本小题正确.
故选D.
考点: 二次函数的性质.

 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案把抛物线y=﹣2x2先向右平移1个单位长度,再向上平移2个单位长度后,所得函数的表达式为( )
| A.y=﹣2(x+1)2+2 | B.y=﹣2(x+1)2﹣2 |
| C.y=﹣2(x﹣1)2+2 | D.y=﹣2(x﹣1)2﹣2 |
如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),顶点坐标为(1,n),与y轴的交点在(0,2)、(0,3)之间(包含端点),则下列结论:①当x>3时,y<0;②3a+b>0;③﹣1≤a≤﹣ ;④3≤n≤4中,正确的是( )。
;④3≤n≤4中,正确的是( )。
| A.①② | B.③④ | C.①④ | D.①③ |
将二次函数 的图象向右平移1个单位,再向上平移2个单位后,所得图象的函数表达式是( )
的图象向右平移1个单位,再向上平移2个单位后,所得图象的函数表达式是( )
A. | B. |
C. | D. |
对于每个x,函数y是y1=-x+6,y2=-2x2+4x+6这两个函数的较小值,则函数y的最大值是
| A.3 | B.4 | C.5 | D.6 |
如图,正方形ABCD的边长为6cm,O是AB的中点,也是抛物线的顶点,OP⊥AB,两半圆的直径分别为OA,OB,抛物线经过C,D两点,且关于OP对称,则图中阴影部分的面积为( )(π取3.14,结果保留两位小数)
| A.7.07cm2 |
| B.3.53cm2 |
| C.14.13cm2 |
| D.10.60cm2 |
二次函数y=x2的图象向上平移2个单位,得到新的图象的二次函数表达式是( )
| A.y=x2-2 |
| B.y=(x-2)2 |
| C.y=x2+2 |
| D.y=(x+2)2 |
西宁中心广场有各种音乐喷泉,其中一个喷水管喷水的最大高度为3米,此时距喷水管的水平距离为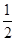 米,在如图所示的坐标系中,这个喷泉的函数关系式是( )
米,在如图所示的坐标系中,这个喷泉的函数关系式是( )
A.y=- +3 +3 | B.y=-3 +3 +3 |
C.y=-12 +3 +3 | D.y=-12 +3 +3 |



