题目内容
21、如图，已知：在Rt△ABC中，∠ACB=90°，AC=4，BC=3，AM=AC，BN=BC．求：（1）AB的长；（2）MN的长．
分析：（1）根据勾股定理：在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方，即可得到AB长；
（2）根据线段的相等关系可得到AM=4，BN=3，再根据线段的和差关系可以得到答案．
（2）根据线段的相等关系可得到AM=4，BN=3，再根据线段的和差关系可以得到答案．
解答：解：（1）∵∠ACB=90°，
∴AB2=AC2+CB2，
∵AC=4，BC=3，
∴AB=5；
（2）∵AM=AC，BN=BC，
∴AM=4，BN=3，
∴AM+BN=AB+MN=7，
∴MN=7-5=2．
∴AB2=AC2+CB2，
∵AC=4，BC=3，
∴AB=5；
（2）∵AM=AC，BN=BC，
∴AM=4，BN=3，
∴AM+BN=AB+MN=7，
∴MN=7-5=2．
点评：此题主要考查了勾股定理，以及线段的和差关系，关键是理清线段之间的关系．
练习册系列答案
相关题目
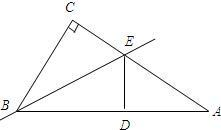如图，已知，在Rt△ABC中，∠C=90°，沿过B点的一条直线BE折叠这个三角形，使C点与AB边上的一点D重合．
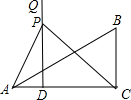重合），过D作DQ⊥AC（DQ与AB在AC的同侧）；点P从D点出发，在射线DQ上运动，连接PA、PC．
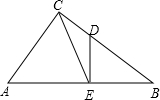如图，已知：在Rt△ABC中，∠ACB=90°，sinB=
如图，已知：在Rt△ABC中，∠ACB=90°，∠B=30°，CD⊥AB于D．