题目内容
【题目】阅读下面材料,并解决问题:
![]() 如图
如图![]() 等边
等边![]() 内有一点P,若点P到顶点A、B、C的距离分别为3,4,5,求
内有一点P,若点P到顶点A、B、C的距离分别为3,4,5,求![]() 的度数.为了解决本题,我们可以将
的度数.为了解决本题,我们可以将![]() 绕顶点A旋转到
绕顶点A旋转到![]() 处,此时
处,此时![]() ≌
≌![]() ,这样就可以利用旋转变换,将三条线段PA、PB、PC转化到一个三角形中,从而求出
,这样就可以利用旋转变换,将三条线段PA、PB、PC转化到一个三角形中,从而求出![]() ______;
______;
![]() 基本运用
基本运用
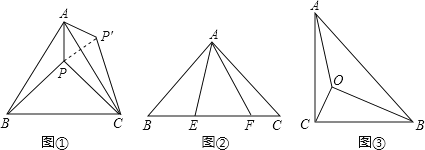
请你利用第![]() 题的解答思想方法,解答下面问题:已知如图
题的解答思想方法,解答下面问题:已知如图![]() ,
,![]() 中,
中,![]() ,
,![]() ,E、F为BC上的点且
,E、F为BC上的点且![]() ,求证:
,求证:![]() ;
;
![]() 能力提升
能力提升
如图![]() ,在
,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点O为
,点O为![]() 内一点,连接AO,BO,CO,且
内一点,连接AO,BO,CO,且![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)![]() .
.
【解析】
![]() 根据旋转变换前后的两个三角形全等,全等三角形对应边相等,全等三角形对应角相等以及等边三角形的判定和勾股定理逆定理解答;
根据旋转变换前后的两个三角形全等,全等三角形对应边相等,全等三角形对应角相等以及等边三角形的判定和勾股定理逆定理解答;
![]() 把
把![]() 绕点A逆时针旋转
绕点A逆时针旋转![]() 得到
得到![]() ,根据旋转的性质可得
,根据旋转的性质可得![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,再求出
,再求出![]() ,从而得到
,从而得到![]() ,然后利用“边角边”证明
,然后利用“边角边”证明![]() 和
和![]() 全等,根据全等三角形对应边相等可得
全等,根据全等三角形对应边相等可得![]() ,再利用勾股定理列式即可得证.
,再利用勾股定理列式即可得证.
![]() 将
将![]() 绕点B顺时针旋转
绕点B顺时针旋转![]() 至
至![]() 处,连接
处,连接![]() ,根据直角三角形
,根据直角三角形![]() 角所对的直角边等于斜边的一半求出
角所对的直角边等于斜边的一半求出![]() ,即
,即![]() 的长,再根据旋转的性质求出
的长,再根据旋转的性质求出![]() 是等边三角形,根据等边三角形的三条边都相等可得
是等边三角形,根据等边三角形的三条边都相等可得![]() ,等边三角形三个角都是
,等边三角形三个角都是![]() 求出
求出![]() ,然后求出C、O、
,然后求出C、O、![]() 、
、![]() 四点共线,再利用勾股定理列式求出
四点共线,再利用勾股定理列式求出![]() ,从而得到
,从而得到![]() .
.
![]() ≌
≌![]() ,
,
![]() 、
、![]() 、
、![]() ,
,
由题意知旋转角![]()
![]() ,
,
![]()
![]() 为等边三角形,
为等边三角形,
P![]() ,
,![]()
![]() ,
,
易证![]()
![]() 为直角三角形,且
为直角三角形,且![]()
![]() ,
,
![]()
![]()
![]() ;
;
故答案为:![]() ;
;
![]() 如图2,把
如图2,把![]() 绕点A逆时针旋转
绕点A逆时针旋转![]() 得到
得到![]() ,
,
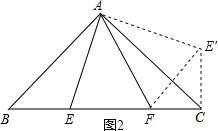
由旋转的性质得,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,
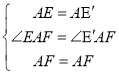 ,
,
![]() ≌
≌![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
由勾股定理得,![]() ,
,
即![]() .
.
![]() 如图3,将
如图3,将![]() 绕点B顺时针旋转
绕点B顺时针旋转![]() 至
至![]() 处,连接
处,连接![]() ,
,
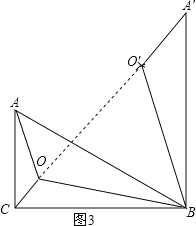
![]() 在
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() 绕点B顺时针方向旋转
绕点B顺时针方向旋转![]() ,
,
![]() 如图所示;
如图所示;
![]() ,
,
![]() 绕点B顺时针方向旋转
绕点B顺时针方向旋转![]() ,得到
,得到![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() 是等边三角形,
是等边三角形,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() 、O、
、O、![]() 、
、![]() 四点共线,
四点共线,
在![]() 中,
中,![]() ,
,
![]() .
.

练习册系列答案
相关题目