Question

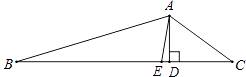
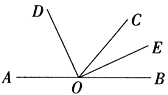
【题目】如图，O是直线AB上一点，OC是任意一条射线，OD,OE分别是∠AOC和∠BOC的平分线，

（1）图中∠BOD的补角是_______________;∠BOE的余角是____________________.

（2）如果∠BOE=∠AOD, 求∠BOE的度数。

Answer 1

【答案】(1) ∠AOD 和∠COD，∠AOD 和∠COD；（2）∠BOE=27°.

【解析】

(1)根据“和为180°的两个角互为补角”、“和为90°的两个角互为余角”进行解答；

(2)根据平角的定义可得∠AOD＋∠BOE=90°，然后再根据∠BOE=∠AOD进行求解.

(1) ∠AOD 和∠COD, ∠AOD 和∠COD ；

(2)∵OD,OE分别是∠AOC与∠BOC的平分线

∴∠AOD＝∠AOC

∠BOE＝∠BOC

∵∠AOC＋∠BOC=180°

∴∠AOD＋∠BOE=90°

∵∠BOE=∠AOD

∴ ∠AOD+ ∠AOD =90°

∴ ∠AOD=63°

∴∠BOE=27°