Question

【题目】在实践中学习：
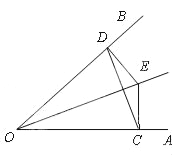
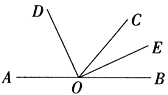
（1）如图1所示：已知AB∥CD，∠ABD=115°，根据 可得出：∠BDC的度数是 ．
（2）如图2所示：已知AB∥CD，∠ABC=25°，∠EDC=40°，求∠BED的度数．

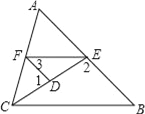
（3）如图3所示：已知MA∥NC，试确定∠A、∠B、∠C和∠E、∠F的关系，并说明理由．
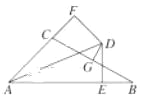
（4）如图4所示：已知AB∥CD，∠ABE=α，∠FCD=β，∠CFE=γ，且BE⊥EF，试确定α、β、γ的关系，请说明理由．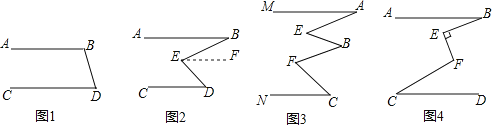

Answer 1

【答案】（1）65°；（2）65°，理由详见解析；（3）∠E+∠F=∠A+∠B+∠C；（4）γ+α=90°+β．.

【解析】

（1）根据两直线平行，同旁内角互补求解；

（2）根据两直线平行，内错角相等求解；

（3）作BH∥AM，如图3，由（2）的结论得到∠E=∠1+∠A，∠F=∠2+∠C，把两式相加得到∠E+∠F=∠1+∠A+∠2+∠C=∠A+∠B+∠C；

（4）作BP∥AB，如图4，由（2）的结论得∠ABE+∠EFP=∠BEF，而∠PFC=∠FCD，所以∠EFP=90°-α，∠PFC=β，把两式相加得到γ=90°-α+β．

（1）∵AB∥CD，

∴∠ABD+∠BDC=180°，

∴∠BDC=180°-115°=65°；

（2）过点E作EF∥AB

∵AB∥CD（已知）∴EF∥CD

∵EF∥AB，EF∥CD

∴∠ABC=∠BEF，∠EDC=∠DEF，

∴∠BEF=25°，∠DEF=40°

即∠BED=65°；

（3）∠A、∠B、∠C和∠E、∠F的关系为∠E+∠F=∠A+∠B+∠C．理由如下：

作BH∥AM，如图3，

由（2）的结论得到∠E=∠1+∠A，∠F=∠2+∠C，

∴∠E+∠F=∠1+∠A+∠2+∠C=∠A+∠B+∠C；

（4）γ+α=90°+β．理由如下：

作BP∥AB，如图4，

由（2）的结论得∠ABE+∠EFP=∠BEF，

而∠PFC=∠FCD，

∴∠EFP=90°-α，∠PFC=β，

∴∠EFP+∠PFC=90°-α+β，

∴γ=90°-α+β，

即γ+α=90°+β．