题目内容
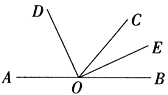
【题目】如图,∠AOC=∠BOC,点P在OC上,PD⊥OA于点D,PE⊥OB于点E.若OD=8,OP=10,则PE的长为( ) 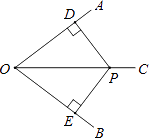
A.5
B.6
C.7
D.8
【答案】B
【解析】解:∵PD⊥OA, ∴∠PDO=90°,
∵OD=8,OP=10,
∴PD= ![]() =6,
=6,
∵∠AOC=∠BOC,点P在OC上,PD⊥OA,PE⊥OB,
∴PE=PD=6.
故选B.
【考点精析】根据题目的已知条件,利用角平分线的性质定理和勾股定理的概念的相关知识可以得到问题的答案,需要掌握定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.

练习册系列答案
相关题目
【题目】某数学兴趣小组在本校九年级学生中以“你最喜欢的一项体育运动”为主题进行了抽样调查,并将调查结果绘制成如图图表:
项目 | 篮球 | 乒乓球 | 羽毛球 | 跳绳 | 其他 |
人数 | a | 12 | 10 | 5 | 8 |
请根据图表中的信息完成下列各题: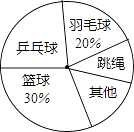
(1)本次共调查学生名;
(2)a= , 表格中五个数据的中位数是;
(3)在扇形图中,“跳绳”对应的扇形圆心角是;
(4)如果该年级有450名学生,那么据此估计大约有人最喜欢“乒乓球”.