题目内容
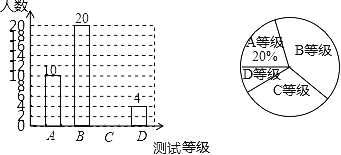
【题目】抚顺某中学为了解八年级学生的体能状况,从八年级学生中随机抽取部分学生进行体能测试,测试结果分为A,B,C,D四个等级.请根据两幅统计图中的信息回答下列问题:
(1)本次抽样调查共抽取了多少名学生?
(2)求测试结果为C等级的学生数,并补全条形图;
(3)若该中学八年级共有700名学生,请你估计该中学八年级学生中体能测试结果为D等级的学生有多少名?
(4)若从体能为A等级的2名男生2名女生中随机的抽取2名学生,做为该校培养运动员的重点对象,请用列表法或画树状图的方法求所抽取的两人恰好都是男生的概率.
【答案】(1)50;(2)16;(3)56(4)见解析
【解析】试题分析:
(1)根据统计图中的信息可知,获得A等的有10人,占抽查总数的20%,由此即可计算出抽查学生的总数;
(2)由(1)中计算结果结合统计图中已知的A、B、D三个等级的人数即可求得C等级的人数,并由此补全条形统计图;
(3)由(1)中求得的被抽查学生的总数及获得D等级的有4人可计算出获得D等级的人数所占的百分比,即可求得800人中可能获得D等级的人数;
(4)设两名男生为A1、A2,两名女生为B1、B2,画出树形图分析即可求得所求概率;
试题解析:
(1)10÷20%=50(名)
答:本次抽样调查共抽取了50名学生.
(2)50-10-20-4=16(名)
答:测试结果为C等级的学生有16名.
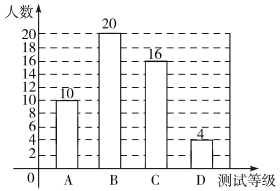
图形统计图补充完整如下图所示:
(3)700×![]() =56(名)
=56(名)
答:估计该中学八年级学生中体能测试结果为D等级的学生有56名.
(4)画树状图法:设体能为A等级的两名男生分别为![]() ,体能为A等级的两名女生分别为
,体能为A等级的两名女生分别为![]() ,
,![]() ,画树状图如下:
,画树状图如下:
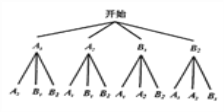
由树状图可知,共有12 种结果,每种结果出现的可能性相同,而抽取的两人都是男生的结果有两种:(![]() ),(
),(![]() ,
,![]() ), ∴P(抽取的两人是男生)=
), ∴P(抽取的两人是男生)=![]() .
.
【题型】解答题
【结束】
20
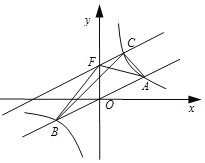
【题目】如图,在平面直角坐标系xOy中,直线AB与x轴交于点A,与y轴交于点B,且OA=3,AB=5.点P从点O出发沿OA以每秒1个单位长的速度向点A匀速运动,到达点A后立刻以原来的速度沿AO返回;点Q从点A出发沿AB以每秒1个单位长的速度向点B匀速运动.伴随着P、Q的运动,DE保持垂直平分PQ,且交PQ于点D,交折线QB﹣BO﹣OP于点E.点P、Q同时出发,当点Q到达点B时停止运动,点P也随之停止.设点P、Q运动的时间是t秒(t>0).
(1)求直线AB的解析式;
(2)在点P从O向A运动的过程中,求△APQ的面积S与t之间的函数关系式(不必写出t的取值范围);
(3)在点E从B向O运动的过程中,完成下面问题:
①四边形QBED能否成为直角梯形?若能,请求出t的值;若不能,请说明理由;
②当DE经过点O时,请你直接写出t的值.
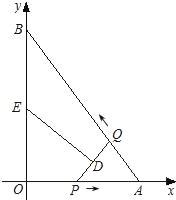
【答案】(1)直线AB的解析式为![]() ;(2)S=﹣
;(2)S=﹣![]() t2+
t2+![]() t;
t;
(3)四边形QBED能成为直角梯形.①t=![]() ;②当DE经过点O时,t=
;②当DE经过点O时,t=![]() 或
或![]() .
.
【解析】分析:(1)首先由在Rt△AOB中,OA=3,AB=5,求得OB的值,然后利用待定系数法即可求得一次函数的解析式;
(2)过点Q作QF⊥AO于点F.由△AQF∽△ABO,根据相似三角形的对应边成比例,借助于方程即可求得QF的长,然后即可求得![]() 的面积S与t之间的函数关系式;
的面积S与t之间的函数关系式;
(3)①分别从DE∥QB与PQ∥BO去分析,借助于相似三角形的性质,即可求得t的值;
②根据题意可知即![]() 时,则列方程即可求得t的值.
时,则列方程即可求得t的值.
详解:(1)在Rt△AOB中,OA=3,AB=5,由勾股定理得![]()
∴A(3,0),B(0,4).
设直线AB的解析式为y=kx+b.
∴![]() .解得
.解得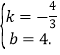
∴直线AB的解析式为![]()
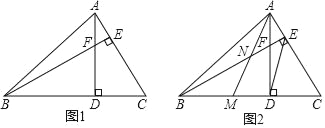
(2)如图1,过点Q作QF⊥AO于点F.
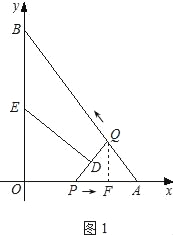
∵AQ=OP=t,∴AP=3t.
由△AQF∽△ABO,得![]()
∴![]()
∴![]()
∴![]()
∴![]()
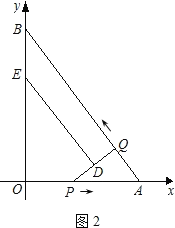
(3)四边形QBED能成为直角梯形,
①如图2,当DE∥QB时,
∴PQ⊥QB,四边形QBED是直角梯形.
此时![]()
由△APQ∽△ABO,得![]()
∴![]()
解得![]()
如图3,当PQ∥BO时,
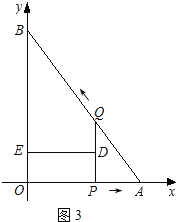
∵DE⊥PQ,
∴DE⊥BO,四边形QBED是直角梯形.
此时![]()
由△AQP∽△ABO,得![]()
即![]()
3t=5(3t),
3t=155t,
8t=15,
解得![]()
(当P从A向0运动的过程中还有两个,但不合题意舍去).
②当DE经过点O时,
∵DE垂直平分PQ,
∴EP=EQ=t,
由于P与Q相同的时间和速度,
∴AQ=EQ=EP=t,
∴∠AEQ=∠EAQ,
∵![]()
∴∠BEQ=∠EBQ,
∴BQ=EQ,
∴![]()
所以![]()
当P从A向O运动时,
过点Q作QF⊥OB于F,
EP=6t,
即EQ=EP=6t,
AQ=t,BQ=5t,
∴![]()
∴![]()
∵![]()
即![]()
解得:![]()
∴当DE经过点O时, ![]() 或
或![]() .
.

 阅读快车系列答案
阅读快车系列答案