题目内容
【题目】如图直角坐标系中，矩形ABCD的边BC在x轴上，点B、D的坐标分别为B（1，0），D（3，3）．
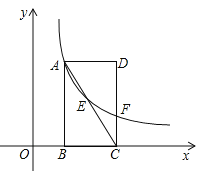
（1）点C的坐标 ；
（2）若反比例函数
的图象经过直线AC上的点E，且点E的坐标为（2，m），求m的值及反比例函数的解析式；
（3）若（2）中的反比例函数的图象与CD相交于点F，连接EF，在直线AB上找一点P，使得
，求点P的坐标．
【答案】（1）C（3，0）；（2）
， 
；（3）（1，0.5）或（1，3.5）
【解析】（1）由D点坐标得；（2）求出直线AC的解析式，把E的坐标代入求出m的值，从而求得反比例函数的解析式；（3）延长FC至M，使CM=
CF，连接EM，过点M作直线MP∥EF交直线AB于P，求出直线EF的解析式，得出直线PM的解析式，从而求出点P的坐标.
解：（1）C（3，0）
（2）设直线AC的解析式为
，则
，解得： 
∴直线AC的解析式为
∵点E（2， 
）在直线AC上， ∴
，
∴点E（2， 
）
∵反比例函数
的图象经过点E，∴
，
∴反比例函数的解析式为 
（3）延长FC至M，使CM=
CF，连接EM，则S△EFM =
S△EFC，M（3，-0.5）
在
中，当
时， 
，∴F（3，1）
过点M作直线MP∥EF交直线AB于P，则S△PEF=S△MEF
设直线EF的解析式为
解得
，∴
设直线PM的解析式为
，代入M（3，－0.5）得： 
∴
当
时
，∴点P（1，0.5）
同理可得点P（1，3.5）
∴点P坐标为（1，0.5）或（1，3.5）
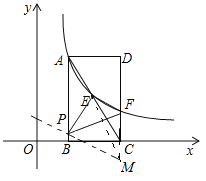
点晴：本题主要考查一次函数与反比例函数的图象和性质并与几何图形结合在一起的综合应用题.其重点是让学生运用待定系数法求函数解析式，难点是第3个问题，通过动手操作让学生猜想并求出满足条件的P的坐标，体现出学生综合运用知识解决实际问题的能力，而突破难点的关键在于利用平行线间的距离处处相等，从而实现等面积的转换.
