题目内容
【题目】如图，一条公路的转弯处是一段圆弧（
）．
（1）用直尺和圆规作出所在圆的圆心O；（要求保留作图痕迹，不写作法）
（2）若的中点C到弦AB的距离为20m，AB=80m，求所在圆的半径．
【答案】（1）见解析；（2）50m．
【解析】
试题分析：（1）连结AC、BC，分别作AC和BC的垂直平分线，两垂直平分线的交点为点O，如图1；
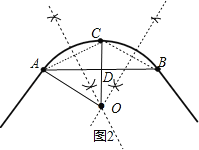
（2）连接OA，OC，OC交AB于D，如图2，根据垂径定理的推论，由C为
的中点得到OC⊥AB，AD=BD=
AB=40，则CD=20，设⊙O的半径为r，在Rt△OAD中利用勾股定理得到r2=（r﹣20）2+402，然后解方程即可．
解：（1）如图1，
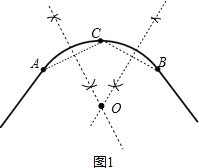
点O为所求；
（2）连接OA，OC，OC交AB于D，如图2，
∵C为
的中点，
∴OC⊥AB，
∴AD=BD=
AB=40，
设⊙O的半径为r，则OA=r，OD=OD﹣CD=r﹣20，
在Rt△OAD中，∵OA2=OD2+BD2，
∴r2=（r﹣20）2+402，解得r=50，
即所在圆的半径是50m．
练习册系列答案
相关题目
【题目】在某项针对18～35岁的青年人每天发微博数量的调查中，设一个人的“日均发微博条数”为m，规定：当m≥10时为A级，当5≤m＜10时为B级，当0≤m＜5时为C级.现随机抽取30个符合年龄条件的青年人开展每人“日均发微博条数”的调查，所抽青年人的“日均发微博条数”的数据如下：
11 | 10 | 6 | 15 | 9 | 16 | 13 | 12 | 0 | 8 | 2 | 8 | 10 | 17 | 6 |
13 | 7 | 5 | 7 | 3 | 12 | 10 | 7 | 11 | 3 | 6 | 8 | 14 | 15 | 12 |
（1）求样本数据中为A级的频率；
（2）试估计1000个18～35岁的青年人中“日均发微博条数”为A级的人数
（3）从样本数据为C级的人中随机抽取2人，用树状图或列表法求抽得2个人的“日均发微博条数”都是3的概率.
