题目内容
【题目】如图，△ABC是边长为6的等边三角形，P是AC边上一动点，由A向C运动(与A、C不重合)，Q是CB延长线上一点，与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合)，过P作PE⊥AB于E，连接PQ交AB于D.
(1)当∠BQD=30°时，求AP的长；
(2)证明：在运动过程中，点D是线段PQ的中点；
(3)当运动过程中线段ED的长是否发生变化？如果不变，求出线段ED的长；如果变化请说明理由.
【答案】（1）2；（2）证明见解析；（3）3.
【解析】试题分析：（1）先判断出∠QPC是直角，再利用含30°的直角三角形的性质得出QC=2PC，建立方程求解决即可；
（2）先作出PF∥BC得出∠PFA=∠FPA=∠A=60°，进而判断出△DQB≌△DPF得出DQ=DP即可得出结论；
（3）利用等边三角形的性质得出EF=
AF，借助DF=DB，即可得出DF=BF，最后用等量代换即可．
试题解析：（1）解：设AP=x，则BQ=x，
∵∠BQD=30°，∠C=60°，
∴∠QPC=90°，
∴QC=2PC，即x+6=2（6-x），
解得x=2，
即AP=2．
（2）证明：如图，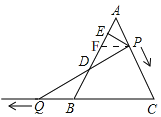
过P点作PF∥BC，交AB于F，
∵PF∥BC，
∴∠PFA=∠FPA=∠A=60°，
∴PF=AP=AF，
∴PF=BQ，
又∵∠BDQ=∠PDF，∠DBQ=∠DFP，
∴△DQB≌△DPF，
∴DQ=DP即D为PQ中点，
（3）运动过程中线段ED的长不发生变化，是定值为3，
理由：∵PF=AP=AF，PE⊥AF，
∴EF=AF，
又∵△DQB≌△DPF，
∴DF=DB，即DF=BF，
∴ED=EF+DF= (AF+BF)=AB=3．
练习册系列答案
相关题目
