题目内容
如图,⊙O的半径为1,圆心在坐标原点,点A的坐标为(-2,0),点B的坐标为(0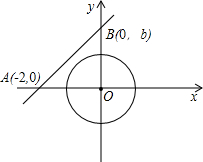 ,b)(b>0).
,b)(b>0).(1)当b为何值时,直线AB与⊙O相离?相切?相交?
(2)当AB与⊙O相切时,求直线AB的解析式?
分析:(1)首先求得相切时的b值,即设AB与⊙O相切于C,连接OC,则OC⊥AB.利用锐角三角函数求得b值,再进一步分情况讨论;
(2)根据(1)中求得相切时点B的坐标,运用待定系数法求解.
(2)根据(1)中求得相切时点B的坐标,运用待定系数法求解.
解答: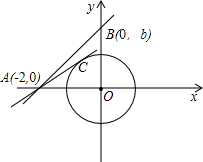 解:(1)设AB与⊙O相切于C,连接OC,则OC⊥AB.
解:(1)设AB与⊙O相切于C,连接OC,则OC⊥AB.
在Rt△AOC中,∵OC=1,OA=2,
∴sin∠OAC=
,
∴∠OAC=30°.
∴OB=OA•tan30°=2•
=
.
∴当b>
时,直线AB与⊙O相离;
当b=
时,直线AB与⊙O相切;
当0<b<
时,直线AB与⊙O相交.
(2)当直线AB与⊙O相切时,点B的坐标为(0,
),
设直线AB的解析式为y=kx+
,
将(-2,0)代入,得0=-2k+
?k=
.
∴直线AB的解析式为y=
x+
.
 解:(1)设AB与⊙O相切于C,连接OC,则OC⊥AB.
解:(1)设AB与⊙O相切于C,连接OC,则OC⊥AB.在Rt△AOC中,∵OC=1,OA=2,
∴sin∠OAC=
| 1 |
| 2 |
∴∠OAC=30°.
∴OB=OA•tan30°=2•
| ||
| 3 |
2
| ||
| 3 |
∴当b>
2
| ||
| 3 |
当b=
2
| ||
| 3 |
当0<b<
2
| ||
| 3 |
(2)当直线AB与⊙O相切时,点B的坐标为(0,
2
| ||
| 3 |
设直线AB的解析式为y=kx+
2
| ||
| 3 |
将(-2,0)代入,得0=-2k+
2
| ||
| 3 |
| ||
| 3 |
∴直线AB的解析式为y=
| ||
| 3 |
2
| ||
| 3 |
点评:此题考查了直线和圆的位置关系与数量之间的联系、锐角三角函数以及待定系数法求函数解析式的方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,⊙O的半径为5,AB=5
如图,⊙O的半径为5,AB=5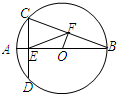 如图,⊙O的半径为3,直径AB⊥弦CD,垂足为E,点F是BC的中点,那么EF2+OF2=
如图,⊙O的半径为3,直径AB⊥弦CD,垂足为E,点F是BC的中点,那么EF2+OF2= 如图,⊙O的半径为
如图,⊙O的半径为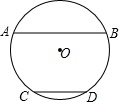 如图,⊙O的半径为13cm,弦AB∥CD,两弦位于圆心O的两侧,AB=24cm,CD=10cm,求AB和CD的距离.
如图,⊙O的半径为13cm,弦AB∥CD,两弦位于圆心O的两侧,AB=24cm,CD=10cm,求AB和CD的距离.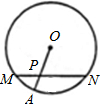 如图,⊙O的半径为5,P是弦MN上的一点,且MP:PN=1:2.若PA=2,则MN的长为
如图,⊙O的半径为5,P是弦MN上的一点,且MP:PN=1:2.若PA=2,则MN的长为