��Ŀ����
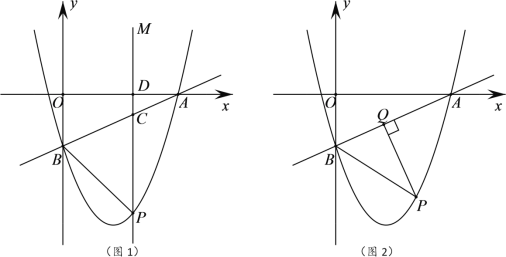
����Ŀ����ͼ��A��B��C��D�ĵ㶼��OO�ϣ���AC����BC������AB��CD��AD����ADC��45�㣮
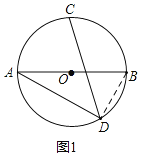
��1����ͼ1��AB����O��ֱ����
��2����ͼ2������B��BE��CD�ڵ�E����F�ڻ�AC�ϣ�����BF��CD�ڵ�G����FGC��2��BAD����֤��BAƽ�֡�FBE��
��3����ͼ3���ڣ�2���������£�MN����O�����ڵ�M����EB���ӳ����ڵ�N������AM����2��MAD+��FBA��135�㣬MN��![]() AB��EN��26�����߶�CD�ij���
AB��EN��26�����߶�CD�ij���

���𰸡���1�������������2�������������3��34
��������
(1)����ֱ������Բ�ܽ���ֱ�Ǽ��ɽ���;
(2)��������,ͨ���뾶��ȵõ�����������,����֪�ġ�FGC��2��BAD�õ�B��G��O��D�ĵ㹲Բ���Ƴ���ODE����OBG���ɽ���;
(3)��������,ͨ��ֱ������Բ�ܽ���ֱ�ǵõ���ACB��90��,����2��MAD+��FBA��135�㣬�õ�AM��DM������֤����ADR�ǵ���ֱ�������Σ���ACR�ա�CBE��AAS�����ı���OEQM�Ǿ��Σ��١�EQN�ǵ���ֱ�������Σ���OER�ǵ���ֱ�������Σ����ͨ�����ɶ������ɽ���.
�⣨1����ͼ1������BD��
��![]() ��
��
���BDC����ADC��45�㣬
���ADB��90�㣬
��AB��ԲO��ֱ����
��2����ͼ2������OG��OD��BD��
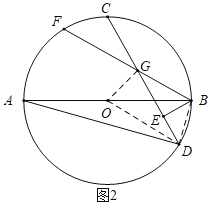
��OA��OD��OB��
���OAD����ODA����OBD����ODB��
���DOB����OAD+��ODA��2��BAD��
�ߡ�FGC��2��BAD��
���DOB����FGC����BGD��
��B��G��O��D�ĵ㹲Բ��
���ODE����OBG��
��BE��CD����BDC��45�㣬
���EBD��45�㣽��EDB��
���OBE����ODE����OBG��
��BAƽ�֡�FBE��
��3����ͼ3������AC��BC��CO��DO��EO��BD��
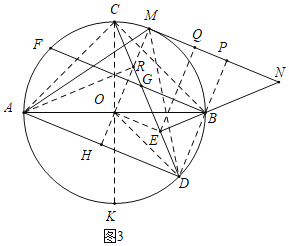
��AC��BC��
��AC��BC��
��ABΪֱ����
���ACB��90�㣬��CAB����CBA��45�㣬CO��AB��
�ӳ�CO��ԲO�ڵ�K�����DOK����OCD+��ODC��2��ODC��2��OBE��2��FBA��
����DM��OM�����MOD��2��MAD��
��2��MAD+��FBA��135�㣬
���MOD+��FBA��135�㣬
��2��MOD+2��FBA��270�㣬
��2��MOD+��DOK��270�㣬
�ߡ�AOM+��DOM+��KOK��270�㣬
���AOM����DOM��
��AM��DM��
����MO���ӳ���AD��H�����MHA����MHD��90�㣬AH��DH��
��MH��BC���ڵ�R������AR����AR��DR��
�ߡ�ADC��45�㣬
���ARD����ARC��90�㣬��ADR�ǵ���ֱ�������Σ�
���BRH����ARH��45��
�ߡ�ACR+��BCE����BCE+��CBE��90�㣬
���ACR����CBE��
���ACR�ա�CBE��AAS����
��CR��BE��ED��
��EQ��MN��Q�����EQN����EQM��90�㣬
����OE����OE��ֱƽ��BD��
��OE��AD��MN��
���ı���OEQM�Ǿ��Σ�
��OM��EQ��OE��MQ��
�ӳ�DB��MN�ڵ�P��
�ߡ�PBN����EBD��45�㣬
���BNP��45�㣬
���EQN�ǵ���ֱ�������Σ�
��EQ��QN��![]() EN��13
EN��13![]() ��
��
��OA��OB��OC��OD��OM�T13![]() ��AB��2OA��26
��AB��2OA��26![]() ��
��
��BC��![]() OC��26��
OC��26��
��MN��![]() AB��20
AB��20![]() ��
��
��OE��MQ��MN��QN��20![]() ��13
��13![]() ��7
��7![]() ��
��
�ߡ�ORE��45�㣬��EOR��90�㣬
���OER�ǵ���ֱ�������Σ�
��RE��![]() OE��14��
OE��14��
��BE��CR��x����CE��14+x��
��Rt��CBE��BC2��CE2+BE2��
��262����x+14��2+x2�����x��10��
��CD��CR+RE+DE��10+14+10��34��