题目内容
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 在
在![]() 外,连接
外,连接![]() ,
,![]() ,且
,且![]() .
.
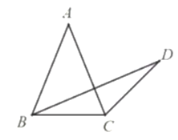
(1)若![]() ,求
,求![]() 的度数;
的度数;
(2)若![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)过点![]() 作
作![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,根据等腰三角形的性质,可设
,根据等腰三角形的性质,可设![]() ,设
,设![]() ,根据三角形外角的性质以及三角形的内角和可得出∠BCD=90°+y,再由
,根据三角形外角的性质以及三角形的内角和可得出∠BCD=90°+y,再由![]() 列方程即可求出y的值,从而得出结果;
列方程即可求出y的值,从而得出结果;
(2)解法一:过点![]() 作
作![]() 交于点
交于点![]() ,在
,在![]() 上取点
上取点![]() 作
作![]() ,证明
,证明![]() ,再结合相似三角形的性质可得出结果;解法二:如图,过点
,再结合相似三角形的性质可得出结果;解法二:如图,过点![]() 作
作![]() 交于点
交于点![]() ,交
,交![]() 延长线于点
延长线于点![]() ,连接
,连接![]() .证明
.证明![]() ,再结合相似三角形的性质可得出结果;解法三:将
,再结合相似三角形的性质可得出结果;解法三:将![]() 沿
沿![]() 翻折得到
翻折得到![]() ,连接
,连接![]() .先证明
.先证明![]() 为等腰直角三角形,再证明
为等腰直角三角形,再证明![]() ,结合相似三角形的性质可得出结果.
,结合相似三角形的性质可得出结果.
解:(1)如图,过点![]() 作
作![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,
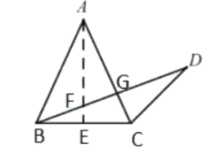
∵![]() ,∴
,∴![]() ,
,
∵![]() ,
,
∴设![]() ,
,
∴![]() ,
,
设![]() ,∴
,∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴![]() 的度数为
的度数为![]() .
.
(2)解法一:如图,过点![]() 作
作![]() 交于点
交于点![]() ,在
,在![]() 上取点
上取点![]() 作
作![]() ,
,
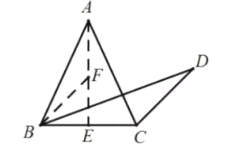
则∠FBE=∠EBF=45°,△BEF为等腰直角三角形.
∵AB=AC,∴BE=CE.
∵![]() ,∴
,∴![]() ,
,
又![]() ,∠AFB+∠BFE=180°,∠ABD=∠BFE=45°,
,∠AFB+∠BFE=180°,∠ABD=∠BFE=45°,
∴![]() ,
,
∴![]() ,
,
故![]() ,即
,即![]() .
.
解法二:如图,过点![]() 作
作![]() 交于点
交于点![]() ,交
,交![]() 延长线于点
延长线于点![]() ,连接
,连接![]() .
.
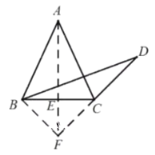
∵![]() 且
且![]() ,∴
,∴![]() ,
,
∴![]() ,∴∠ECF=∠EFC=45°,∴
,∴∠ECF=∠EFC=45°,∴![]() ,
,
又![]() ,则
,则![]() ,
,
故![]() 且
且![]() ,
,
∴∠ABD=∠EBF,
∴![]() .
.
∴![]() ,
,
∴![]() ,即
,即![]() .
.
解法三:如图,将![]() 沿
沿![]() 翻折得到
翻折得到![]() ,连接
,连接![]() .
.
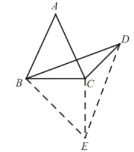
∵![]() 且
且![]() ,∴
,∴![]() =∠DCE,
=∠DCE,
∴![]() ,又
,又![]() ,即
,即![]() 为等腰直角三角形.
为等腰直角三角形.
∴∠CBE=∠ABD=45°,∴∠ABC=∠DBE,
又![]() ,
,![]() ,
,
∴∠ACB=∠DEB,
∴![]() ,
,
∴![]() ,故
,故![]() .
.

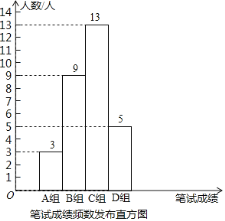
【题目】某公司为了到高校招聘大学生,为此设置了三项测试:笔试、面试、实习.学生的最终成绩由笔试面试、实习依次按3:2:5的比例确定.公司初选了若干名大学生参加笔试,面试,并对他们的两项成绩分别进行了整理和分析.下面给出了部分信息:
①公司将笔试成绩(百分制)分成了四组,分别为A组:60≤x<70,B组:70≤x<80,C组:80≤x<90,D组:90≤x<100;并绘制了如下的笔试成绩频数分布直方图.其中,C组的分数由低到高依次为:80,81,82,83,83,84,84,85,86,88,88,88,89.
②这些大学生的笔试、面试成绩的平均数、中位数、众数、最高分如下表:
平均数 | 中位数 | 众数 | 最高分 | |
笔试成绩 | 81 | m | 92 | 97 |
面试成绩 | 80.5 | 84 | 86 | 92 |
根据以上信息,回答下列问题:
(1)这批大学生中笔试成绩不低于88分的人数所占百分比为 .
(2)m= 分,若甲同学参加了本次招聘,他的笔试、面试成绩都是83分,那么该同学成绩排名靠前的是 成绩,理由是 .
(3)乙同学也参加了本次招聘,笔试成绩虽不是最高分,但也不错,分数在D组;面试成绩为88分,实习成绩为80分由表格中的统计数据可知乙同学的笔试成绩为 分;若该公司最终录用的最低分数线为86分,请通过计算说明,该同学最终能否被录用?