题目内容
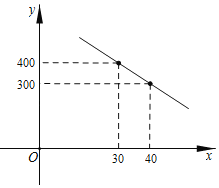
【题目】某童装店购进一批20元/件的童装,由销售经验知,每天的销售量y(件)与销售单价x(元)之间存在如图的一次函数关系.
(1)求y与x之间的函数关系;
(2)当销售单价定为多少时,每天可获得最大利润,最大利润是多少?
【答案】(1)y=﹣10x+700;(2)销售单价为45元时,每天可获得最大利润,最大利润为6250元
【解析】
(1)由一次函数的图象可知过(30,400)和(40,300),利用待定系数法可求得y与x的关系式;
(2)利用x可表示出p,再利用二次函数的性质可求得p的最大值.
(1)设一次函数解析式为y=kx+b(k≠0),
由图象可知一次函数的过(30,400)和(40,300),
代入解析式可得![]() ,
,
解得:![]() ,
,
∴y与x的函数关系式为y=﹣10x+700;
(2)设利润为p元,由(1)可知每天的销售量为y千克,
∴p=y(x﹣20)=(﹣10x+700)(x﹣20)=﹣10x2+900x﹣14000=﹣10(x﹣45)2+6250.
∵﹣10<0,
∴p=﹣10(x﹣45)2+6250是开口向下的抛物线,
∴当x=45时,p有最大值,最大值为6250元,
即销售单价为45元时,每天可获得最大利润,最大利润为6250元.

练习册系列答案
相关题目