Question

【题目】在平面直角坐标系xOy中，将任意两点P（x1，y1）与Q（x2，y2）之间的“直距”定义为：DPQ=|x1﹣x2|+|y1﹣y2|．

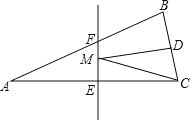
例如：点M（1，﹣2），点N（3，﹣5），则DMN=|1﹣3|+|﹣2﹣（﹣5）|=5．已知点A（1，0）、点B（﹣1，4）．

（1）则DAO=　　，DBO=　　；

（2）如果直线AB上存在点C，使得DCO为2，请你求出点C的坐标；

（3）如果⊙B的半径为3，点E为⊙B上一点，请你直接写出DEO的取值范围．

Answer 1

【答案】（1）1；5；（2）（0，2）或（，﹣ ）；（3）4﹣2≤DEO≤5+3．

【解析】

（1）根据“直距”定义结合点A、B的坐标，即可求出结论；

（2）根据点A、B的坐标，利用待定系数法求出直线AB的解析式，设点C的坐标为（m，-2m+2），根据DCO=2，即可得出关于m的含绝对值符号的一元一次方程，解之即可得出结论；

（3）设点E的坐标为（x，y），则当点E在第一象限时，DEO=x+y，当点E在第二象限时，DEO=y-x．作直线y=x、y=-x的平行线（与），找出这些平行线与y轴交点的纵坐标的最值即可得出结论．

（1）DAO=|1-0|+|0-0|=1；DBO=|-1-0|+|4-0|=5．

故答案为：1；5．

（2）设直线AB的解析式为y=kx+b（k≠0），

将点A（1，0）、B（-1，4）代入y=kx+b，

，解得：，

∴直线AB的解析式为y=-2x+2．

设点C的坐标为（m，-2m+2），

∵DCO=2，

∴|m-0|+|-2m+2-0|=2，

解得：m1=0，m2=，

∴点C的坐标为（0，2）或（，-）．

（3）∵点B的坐标为（-1，4），⊙B的半径为3，

∴⊙B位于第一、二象限，

设点E的坐标为（x，y），

∴当点E在第一象限时，DEO=x+y，当点E在第二象限时，DEO=y-x．

设⊙B与y轴交于点N（下面的交点），连接BN，过点B作BM⊥y轴于点M，

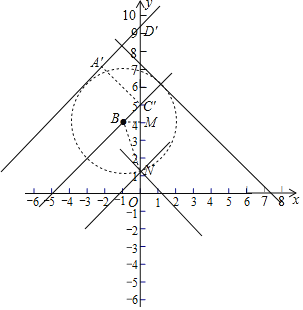
在Rt△BMN中，BM=1，BN=3，

∴MN=，

∴ON=4-2；

设直线y=x+b经过点B，

∵点B的坐标为（-1，4），

∴4=-1+b，解得：b=5，

∴点C′的坐标为（0，5）．

过点C′作A′D′⊥直线A′D′与点A′，则A′C′=3，

又∵△A′C′D′为等腰直角三角形，

∴C′D′=3，

∴OD′=5+3．

∴4-2≤DEO≤5+3．