题目内容
如图,直线y=kx+b(k≠0)与x轴、y轴分别交于点A(3,0),B(0,| 3 |
(1)求直线y=kx+b的解析式及∠BAO,∠PBO的度数;
(2)若⊙P沿x轴向右移动,当⊙P与该直线相切时,求点P的坐标;
(3)在⊙P沿x轴向右移动的过程中,当⊙P与该直线相交时,求横坐标为整数的点P的坐标.
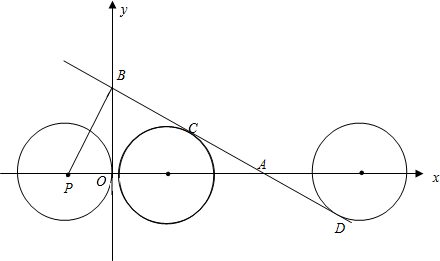
分析:(1)要求直线的解析式,用待定系数法将已知点的坐标代入就直接可以求出解析式.
(2)连接CP1,根据相似三角形的性质求出AP1的值,求出P1O,就可以求出P1的坐标.
(3)利用(2)的方法求出P2的坐标,从而可以求出P1P2之间的整数点的坐标.
(2)连接CP1,根据相似三角形的性质求出AP1的值,求出P1O,就可以求出P1的坐标.
(3)利用(2)的方法求出P2的坐标,从而可以求出P1P2之间的整数点的坐标.
解答:解:(1)把A、B的坐标分别代入解析式为:
,
解得:
,
∴直线y=kx+b的解析式为:y=-
x+
,
∵tan∠BAO=
,∴∠BAO=30°,
∵tan∠PBO=
,∴∠PBO=30°,
(2)连接CP1在直角三角形PBO和直角三角形ABO中由勾股定理可以求出:
AB=2
,OB=
,AO=3,OP=1,PB=2,
由勾股定理的逆定理可知△ABP为直角三角形.
∴连接CP1⊥AB,
∴△ABP∽△ACP1
∴
=
∴
=
∴AP1=2
同理可以求出AP2=2
∴OP1=1,OP2=5
∴当⊙P与该直线相切时,P(1,0)或P(5,0)
(3)由(2)可知当点P在P1、P2之间移动时,⊙P与直线相交,
∵大于1小于5的整数有:2,3,4.
∴⊙P与该直线相交时,横坐标为整数的点P的坐标有:P(2,O),P(3,0),(或4,0).

|
解得:
|
∴直线y=kx+b的解析式为:y=-
| ||
| 3 |
| 3 |
∵tan∠BAO=
| ||
| 3 |
∵tan∠PBO=
| ||
| 3 |
(2)连接CP1在直角三角形PBO和直角三角形ABO中由勾股定理可以求出:
AB=2
| 3 |
| 3 |
由勾股定理的逆定理可知△ABP为直角三角形.
∴连接CP1⊥AB,
∴△ABP∽△ACP1
∴
| CP1 |
| PA |
| AP1 |
| AP |
∴
| 1 |
| 2 |
| AP1 |
| 4 |
∴AP1=2
同理可以求出AP2=2
∴OP1=1,OP2=5
∴当⊙P与该直线相切时,P(1,0)或P(5,0)
(3)由(2)可知当点P在P1、P2之间移动时,⊙P与直线相交,
∵大于1小于5的整数有:2,3,4.
∴⊙P与该直线相交时,横坐标为整数的点P的坐标有:P(2,O),P(3,0),(或4,0).

点评:本题是一次函数的综合试题,考查了用待定系数法求一次函数的解析式,勾股定理的运用,圆切线的性质,30°的特殊直角三角形的性质

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
 如图,直线y=kx+b经过点A(0,3),B(-2,0),则k的值为( )
如图,直线y=kx+b经过点A(0,3),B(-2,0),则k的值为( )| A、3 | ||
B、
| ||
C、
| ||
D、-
|
 如图,直线y=kx+b经过A(2,1),B(-1,-2)两点,则不等式
如图,直线y=kx+b经过A(2,1),B(-1,-2)两点,则不等式| 1 |
| 2 |
| A、x<2 |
| B、x>-1 |
| C、x<1或x>2 |
| D、-1<x<2 |
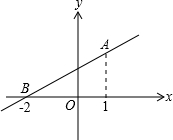 如图,直线y=kx+b经过A(1,2)和B(-2,0)两点,则不等式组-x+3≥kx+b>0的解集为
如图,直线y=kx+b经过A(1,2)和B(-2,0)两点,则不等式组-x+3≥kx+b>0的解集为 7、如图,直线y=kx+b和y=mx都经过点A(-1,-2),则不等式mx<kx+b的解集为( )
7、如图,直线y=kx+b和y=mx都经过点A(-1,-2),则不等式mx<kx+b的解集为( ) 16、如图,直线y=kx-1经过点(2,1),则不等式0≤x<2kx+2的解集为
16、如图,直线y=kx-1经过点(2,1),则不等式0≤x<2kx+2的解集为