��Ŀ����
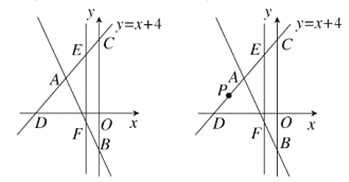
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��![]() ��
��![]() �ᡢ
�ᡢ![]() ��ֱ��ڵ�D��C��ֱ��AB��
��ֱ��ڵ�D��C��ֱ��AB��![]() �ύ�ڵ�
�ύ�ڵ�![]() ����ֱ��CD���ڵ�
����ֱ��CD���ڵ�![]() ��
��
��1����ֱ��AB�Ľ���ʽ��
��2����E������CD��һ���㣬����E��![]() �ᣬ��ֱ��AB�ڵ�F������
�ᣬ��ֱ��AB�ڵ�F������![]() ��
��![]() ��
��![]() ��
��![]() Ϊ������ı�����ƽ���ı��Σ��������E�����ꣻ
Ϊ������ı�����ƽ���ı��Σ��������E�����ꣻ
��3����P������CD��һ���㣬��ƽ�����Ƿ���ڵ�Q��ʹ��B��C��P��QΪ������ı��������Σ������ڣ���ֱ��д�����������ĵ�Q�ĸ���������һ����Q�����ꣻ����˵�����ɣ�
���𰸡���1��![]() ����2����E������Ϊ
����2����E������Ϊ![]() ��
��![]() ����3�����������ĵ�Q��3��������Ϊ��3��1������-6��4����
����3�����������ĵ�Q��3��������Ϊ��3��1������-6��4����![]()
��������
��1����ȷ����A�����꣬�����ô���ϵ�������ɵó����ۣ�
��2���ȱ�ʾ��EF=|a+4-��-2a-2��|=|3a+6|��������������|3a+6|=4����⼴�ɵó����ۣ�
��3��������������������ε����ʺ��е����깫ʽ���ɵó����ۣ�
�⣺��1������![]() ��
��![]() �ϣ�
�ϣ�
��![]() �����
�����![]() ��
��
����A��������-2��2����
��ֱ��AB�Ľ���ʽΪ![]() ��
��
��![]() ��
��
���![]() ��
��
��ֱ��AB�Ľ���ʽΪ![]() ��
��
��2�������⣬���E������Ϊ![]() ����
����
��![]() �ᣬ��F��ֱ��
�ᣬ��F��ֱ��![]() �ϣ�
�ϣ�
����F������Ϊ![]() ��
��
��![]() ��
��
���Ե�![]() ��
��![]() ��
��![]() ��
��![]() Ϊ������ı�����ƽ���ı��Σ���
Ϊ������ı�����ƽ���ı��Σ���![]() ����
����![]() ��
��
��ֱ��![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() ��
��
����![]() ��������0��4����
��������0��4����
��![]() ����
����![]() ��
��
��ã�![]() ��
��![]() ��
��
����E������Ϊ![]() ��
��![]() ��
��
��3��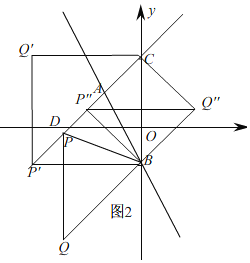
��ͼ2����BCΪ�Խ���ʱ����P��Q����BC�Ĵ�ֱƽ���ߣ��ҵ�P�͵�Q����BC�Գƣ�
��B��0��-2����C��0��4����
����P��������Ϊ1��
��y=1����y=x+4����x+4=1��
��x=-3��
��![]() ��-3��1����
��-3��1����
��![]() ��3��1��
��3��1��
��CP�ǶԽ���ʱ��CP��BQ�Ĵ�ֱƽ���ߣ���Q��m��n����
��BQ���е�����Ϊ![]() ��
��
����ֱ��y=x+4�У���![]() ����
����
��CQ=CB��
��![]() ����
����
�����٢��ã�
![]() ���ᣩ��
���ᣩ��![]() ��
��
��![]() ��-6��4����
��-6��4����
��PB�ǶԽ���ʱ��PC=BA=6��
��P��c��c+4����
��![]() ��
��
��![]() ���ᣩ��
���ᣩ��![]() ��
��
��P![]() ��
��
��Q��d��e��
�� ��
��
��![]() ��
��
��Q![]() ��
��
���������ĵ�Q��3��������Ϊ��3��1������-6��4����![]() ��
��

 ����Ӣ��ϵ�д�
����Ӣ��ϵ�д�����Ŀ��ijУ����ȫ�ж������ݽ�������ѡ����������ѡ�����ɼ����С���С����λͬѧ����ѡ1�˲μ�ȫ�е��ܾ��������˵�ѡ�����ɼ����£���λ���֣���
���� | ���� | ��ͨ�� | �ݽ����� | |
�� | 85 | 70 | 80 | 85 |
�� | 95 | 70 | 75 | 80 |
��1����Ҫ������ռ40%������ռ10%����ͨ��ռ20%���ݽ�����ռ30%�����ܷ֣���λѡ�ֽ�ʤ����
��2����ί�������С���С��ͬѧ���������⡢��ͨ�����ݽ���������ɼ���ƽ���ֶ���80�֣�С��ijɼ�����Ϊ![]() ���������С���ɼ��ķ����˵����Ҫѡ�ɸ��������ʾ����ѡ�ֲ�������λѡ�ֽ�ʤ����
���������С���ɼ��ķ����˵����Ҫѡ�ɸ��������ʾ����ѡ�ֲ�������λѡ�ֽ�ʤ����
����Ŀ��Խ��Խ����������Ÿ��ת�ˣ������˻����Ǯת�����п��������֡�
��2016��3��l����ÿ�����˻���������1000Ԫ��������ֶ�ȣ����ۼ����ֽ���1000Ԫʱ���ۼ����ֽ���1000Ԫ�IJ�����֧��0.1%�������ѣ��Ժ�ÿ������֧����������Ϊ���ֽ���0.1%.
��1��С���ڽ����1�ν��������֣����Ϊl600Ԫ������֧��������_________Ԫ��
��2��С����2016��3��1���������Լ������˻�������3�Σ�3�����ֽ��������ѷֱ����£�
��1�� | ��2�� | ��3�� | |
���ֽ�Ԫ�� | A | b |
|
�����ѣ�Ԫ�� | 0 | 0.4 | 3.4 |
�ʣ�С��3�����ֽ����Ƕ���Ԫ��
��3������������С��0.1Ԫ�ģ�����0.1Ԫ��ȡ�������ֲ���100Ԫ������100Ԫ��ȡ�����ѣ�.С�������������Σ�ÿ�����ֽ�����������֧��������2.4Ԫ����һ������900Ԫ����С��ڶ������ֽ��ķ�Χ.