ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΒ»±Ώ![]() ÷–Θ§±Ώ
÷–Θ§±Ώ![]() άεΟΉΘ§»τΕ·Βψ
άεΟΉΘ§»τΕ·Βψ![]() ¥”Βψ
¥”Βψ![]() ΩΣ ΦΘ§Α¥
ΩΣ ΦΘ§Α¥![]() ΒΡ¬ΖΨΕ‘ΥΕ·Θ§«“ΥΌΕ»ΈΣ1άεΟΉ/ΟκΘ§…ηΒψ
ΒΡ¬ΖΨΕ‘ΥΕ·Θ§«“ΥΌΕ»ΈΣ1άεΟΉ/ΟκΘ§…ηΒψ![]() ΒΡ‘ΥΕ· ±ΦδΈΣ
ΒΡ‘ΥΕ· ±ΦδΈΣ![]() ΟκΘ°
ΟκΘ°
Θ®1Θ©Β±![]() ±Θ§≈–Εœ
±Θ§≈–Εœ![]() ”κ
”κ![]() ΒΡΈΜ÷ΟΙΊœΒΘ§≤ΔΥΒΟςάμ”…ΘΜ
ΒΡΈΜ÷ΟΙΊœΒΘ§≤ΔΥΒΟςάμ”…ΘΜ
Θ®2Θ©Β±![]() ΒΡΟφΜΐΈΣ
ΒΡΟφΜΐΈΣ![]() ΟφΜΐΒΡ“ΜΑκ ±Θ§«σ
ΟφΜΐΒΡ“ΜΑκ ±Θ§«σ![]() ΒΡ÷ΒΘΜ
ΒΡ÷ΒΘΜ
Θ®3Θ©Νμ”–“ΜΒψ![]() Θ§¥”Βψ
Θ§¥”Βψ![]() ΩΣ ΦΘ§Α¥
ΩΣ ΦΘ§Α¥![]() ΒΡ¬ΖΨΕ‘ΥΕ·Θ§«“ΥΌΕ»ΈΣ
ΒΡ¬ΖΨΕ‘ΥΕ·Θ§«“ΥΌΕ»ΈΣ![]() άεΟΉ/ΟκΘ§»τ
άεΟΉ/ΟκΘ§»τ![]() ΓΔ
ΓΔ![]() ΝΫΒψΆ§ ±≥ωΖΔΘ§Β±
ΝΫΒψΆ§ ±≥ωΖΔΘ§Β±![]() ΓΔ
ΓΔ![]() ÷–”–“ΜΒψΒΫ¥ο÷’Βψ ±Θ§Νμ“ΜΒψ“≤ΆΘ÷Ι‘ΥΕ·Θ°Β±
÷–”–“ΜΒψΒΫ¥ο÷’Βψ ±Θ§Νμ“ΜΒψ“≤ΆΘ÷Ι‘ΥΕ·Θ°Β±![]() ΈΣΚΈ÷Β ±Θ§÷±œΏ
ΈΣΚΈ÷Β ±Θ§÷±œΏ![]() Α―
Α―![]() ΒΡ÷ή≥ΛΖ÷≥…œύΒ»ΒΡΝΫ≤ΩΖ÷Θ°
ΒΡ÷ή≥ΛΖ÷≥…œύΒ»ΒΡΝΫ≤ΩΖ÷Θ°
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() Θ§άμ”…ΦϊΫβΈωΘΜΘ®2Θ©
Θ§άμ”…ΦϊΫβΈωΘΜΘ®2Θ©![]() ΒΡ÷ΒΈΣ9Μρ15ΘΜΘ®3Θ©Β±
ΒΡ÷ΒΈΣ9Μρ15ΘΜΘ®3Θ©Β±![]() ΈΣ
ΈΣ![]() Μρ
Μρ![]() Οκ ±Θ§÷±œΏ
Οκ ±Θ§÷±œΏ![]() Α―
Α―![]() ΒΡ÷ή≥ΛΖ÷≥…œύΒ»ΒΡΝΫ≤ΩΖ÷.
ΒΡ÷ή≥ΛΖ÷≥…œύΒ»ΒΡΝΫ≤ΩΖ÷.
ΓΨΫβΈωΓΩ
Θ®1Θ©![]() Θ§Υυ“‘
Θ§Υυ“‘![]() Θ§Εχ
Θ§Εχ![]() ΗυΨίΒ»―ϋ»ΐΫ«–Έ»ΐœΏΚœ“ΜΩ…ΒΟ
ΗυΨίΒ»―ϋ»ΐΫ«–Έ»ΐœΏΚœ“ΜΩ…ΒΟ![]() ΘΜ
ΘΜ
Θ®2Θ©Ζ÷Β±Βψ![]() ΈΣ
ΈΣ![]() ÷–ΒψΚΆΒ±Βψ
÷–ΒψΚΆΒ±Βψ![]() ΈΣ
ΈΣ![]() ÷–Βψ ±Ζ÷±πΦΤΥψΤδ¬Ζ≥ΧΘ§ΫχΕχ«σΤδ ±ΦδtΘΜ
÷–Βψ ±Ζ÷±πΦΤΥψΤδ¬Ζ≥ΧΘ§ΫχΕχ«σΤδ ±ΦδtΘΜ
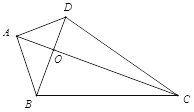
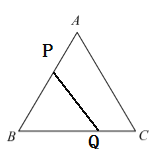
Θ®3Θ©”…”ΎΒψQ¥”CΩΣ ΦΘ§Α¥![]() ΒΡ¬ΖΨΕ‘ΥΕ·Θ§”κΒψPΆ§ ±≥ωΖΔΘ§«“ΤδΥΌΕ» «ΒψPΒΡ1.5±ΕΘ§Υυ“‘Β±ΒψQΒΫ¥ο÷’ΒψC ±Θ§ΒψPΗ’ΒΫ¥οΒψAΘ§Φ¥ΒψP÷ΜΡή‘ΎœΏΕΈBCΚΆAB…œΘ§Ι ÷±œΏPQΑ―
ΒΡ¬ΖΨΕ‘ΥΕ·Θ§”κΒψPΆ§ ±≥ωΖΔΘ§«“ΤδΥΌΕ» «ΒψPΒΡ1.5±ΕΘ§Υυ“‘Β±ΒψQΒΫ¥ο÷’ΒψC ±Θ§ΒψPΗ’ΒΫ¥οΒψAΘ§Φ¥ΒψP÷ΜΡή‘ΎœΏΕΈBCΚΆAB…œΘ§Ι ÷±œΏPQΑ―![]() ΒΡ÷ή≥ΛΖ÷≥…œύΒ»ΒΡΝΫ≤ΩΖ÷ ±Ζ÷ΝΫ÷÷«ιΩωΘΚΒ±Βψ
ΒΡ÷ή≥ΛΖ÷≥…œύΒ»ΒΡΝΫ≤ΩΖ÷ ±Ζ÷ΝΫ÷÷«ιΩωΘΚΒ±Βψ![]() ‘Ύ±Ώ
‘Ύ±Ώ![]() …œΘ§Βψ
…œΘ§Βψ![]() ‘Ύ±Ώ
‘Ύ±Ώ![]() …œΚΆΒ±Βψ
…œΚΆΒ±Βψ![]() ‘Ύ±Ώ
‘Ύ±Ώ![]() …œΘ§Βψ
…œΘ§Βψ![]() ‘Ύ±Ώ
‘Ύ±Ώ![]() …œΘ§Ζ÷±πΦΤΥψ«σΫβΦ¥Ω….
…œΘ§Ζ÷±πΦΤΥψ«σΫβΦ¥Ω….
ΫβΘΚΘ®1Θ©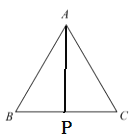
≈–ΕœΘΚ![]() Θ§
Θ§
άμ”…»γœ¬ΘΚ
“ρΈΣ![]() Θ§Υυ“‘
Θ§Υυ“‘![]()
”÷“ρΈΣ![]()
Υυ“‘![]()
Θ®2Θ©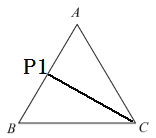
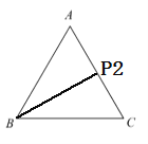
Β±Βψ![]() ΈΣ
ΈΣ![]() ÷–Βψ ±Θ§œ‘»Μ
÷–Βψ ±Θ§œ‘»Μ![]() Θ§Υυ“‘
Θ§Υυ“‘![]()
Β±Βψ![]() ΈΣ
ΈΣ![]() ÷–Βψ ±Θ§œ‘»Μ
÷–Βψ ±Θ§œ‘»Μ![]() Θ§Υυ“‘
Θ§Υυ“‘![]()
Υυ“‘![]() ΒΡ÷ΒΈΣ9Μρ15
ΒΡ÷ΒΈΣ9Μρ15
Θ®3Θ©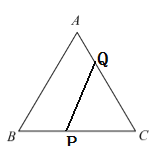
Β±Βψ![]() ‘Ύ±Ώ
‘Ύ±Ώ![]() …œΘ§«“Βψ
…œΘ§«“Βψ![]() ‘Ύ±Ώ
‘Ύ±Ώ![]() …œ ±Θ§
…œ ±Θ§![]() Θ§
Θ§![]()
‘ρ![]() Θ§Υυ“‘
Θ§Υυ“‘![]()
Β±Βψ![]() ‘Ύ±Ώ
‘Ύ±Ώ![]() …œΘ§«“Βψ
…œΘ§«“Βψ![]() ‘Ύ±Ώ
‘Ύ±Ώ![]() …œ ±Θ§
…œ ±Θ§![]()
![]() Θ§
Θ§
‘ρ![]() Θ§Υυ“‘
Θ§Υυ“‘![]()
Υυ“‘Β±![]() ΈΣ
ΈΣ![]() Μρ
Μρ![]() Οκ ±Θ§÷±œΏ
Οκ ±Θ§÷±œΏ![]() Α―
Α―![]() ΒΡ÷ή≥ΛΖ÷≥…œύΒ»ΒΡΝΫ≤ΩΖ÷.
ΒΡ÷ή≥ΛΖ÷≥…œύΒ»ΒΡΝΫ≤ΩΖ÷.

 ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ
ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ –Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗ
–Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗΓΨΧβΡΩΓΩΡ≥±ωΙί”Β”–ΩΆΖΩ90ΦδΘ§Ψ≠”Σ÷–ΖΔœ÷ΘΚΟΩΧλ»κΉΓΒΡΩΆΖΩ ΐyΘ®ΦδΘ©”κΖΩΦέxΘ®‘ΣΘ©Θ®180ΓήxΓή300Θ©¬ζΉψ“Μ¥ΈΚ· ΐΙΊœΒΘ§≤ΩΖ÷Ε‘”Π÷Β»γœ¬±μΘΚ
xΘ®‘ΣΘ© | 200 | 240 | 270 | 300 |
yΘ®ΦδΘ© | 90 | 70 | 55 | 40 |
Θ®1Θ©«σy”κx÷°ΦδΒΡΚ· ΐ±μ¥ο ΫΘΜ
Θ®2Θ©“―÷ΣΟΩΦδ»κΉΓΒΡΩΆΖΩΘ§±ωΙίΟΩ»’–η÷ß≥ωΗς÷÷Ζ―”Ο100‘ΣΘΜΟΩ»’Ω’÷ΟΒΡΩΆΖΩΘ§±ωΙίΟΩ»’–η÷ß≥ω60‘ΣΘ§Β±ΖΩΦέΈΣΕύ…Ό‘Σ ±Θ§±ωΙίΒ±»’άϊ»σΉν¥σΘΩ«σ≥ωΉν¥σ÷ΒΘ°Θ®±ωΙίΒ±»’άϊ»σ=Β±»’ΖΩΖ― ’»κ©¹Β±»’÷ß≥ωΘ©