题目内容
【题目】如图,在△ABC中,AB=AC,点E在线段AC上,D在AB的延长线上,连接DE交BC于F,过E作EG⊥BC于G.
(1)下列两个关系式:①DB=EC,②DF=EF,请你选择一个做为条件,另一个做为结论构成一个正确的命题,并给予证明.
你选择的条件是 ,结论是 .(只需填序号)
(2)在(1)的条件下,求证:FG=BC/2.
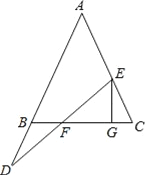
【答案】(1)条件是①DB=EC,结论是②DF=EF,理由见解析;(2)见解析
【解析】试题分析:(1)条件是①DB=EC,结论是②DF=EF.(也可以填条件是②,结论是①).只要证明![]() ,即可解决问题.
,即可解决问题.
(2)由(1)可知, ![]() 推出
推出![]() ,由
,由![]() ,推出
,推出![]() 即可推出
即可推出![]()
试题解析:(1)条件是①DB=EC,结论是②DF=EF.(也可以填条件是②,结论是①).
理由:如图作, ![]() 交BC于H.
交BC于H.

∵![]()
∴∠ABC=∠EHC,∠D=∠HEF,
∵AB=AC,
∴∠ABC=∠C=∠EHC,
∴EH=EC=BD,
在△FBD和△FEH中,

![]()
∴DF=EF.
(2)证明:由(1)可知,EH=EC,EG⊥HC,
∴GH=GC,
![]()
![]()
∴![]()

练习册系列答案
相关题目