题目内容
如图1，是用硬纸板做成的两个全等的直角三角形，两直角边的长分别为a和b，斜边长为c，图2是以c为直角边的等腰直角三角形，用图1和图2可拼成图3的图形（1）请指出图3是什么图形，并用它证明勾股定理．
（2）请用若干个图1中的直角三角形拼成一个能证明勾股定理图形．（画出图形，不用证明）
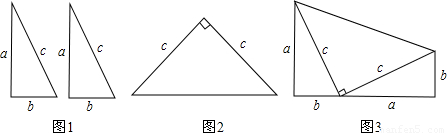
【答案】分析：（1）根据图形可知是梯形，再根据梯形的面积等于三个直角三角形的面积的和，列式整理即可证明；
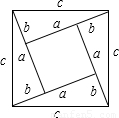
（2）取四个直角三角形，以斜边c为边长组成正方形，中间空出的是一个小正方形，然后利用大正方形的面积等于四个直角三角形的面积加上中间小正方形的面积，列式整理即可得证．
解答：解：（1）是梯形，
梯形的面积=
（a+b）（a+b）=2×
×ab+
c2，
（a2+2ab+b2）=ab+
c2，
a2+b2=c2；
（2）如图所示，图形可以证明．
点评：本题考查了勾股定理的证明，根据图形的面积列式整理即可，（2）中图形答案不唯一，富有创造性，只要是根据面积可以推出勾股定理即可．
（2）取四个直角三角形，以斜边c为边长组成正方形，中间空出的是一个小正方形，然后利用大正方形的面积等于四个直角三角形的面积加上中间小正方形的面积，列式整理即可得证．
解答：解：（1）是梯形，
梯形的面积=
（a+b）（a+b）=2××ab+c2，（a2+2ab+b2）=ab+c2，a2+b2=c2；
（2）如图所示，图形可以证明．
点评：本题考查了勾股定理的证明，根据图形的面积列式整理即可，（2）中图形答案不唯一，富有创造性，只要是根据面积可以推出勾股定理即可．
练习册系列答案
53随堂测系列答案
相关题目
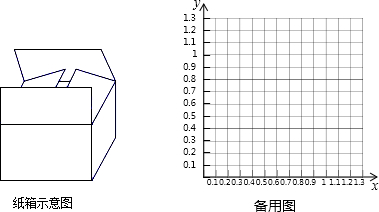
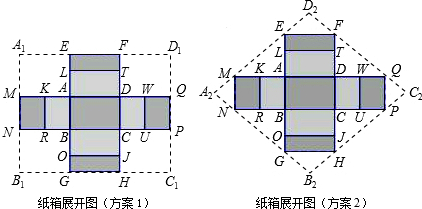
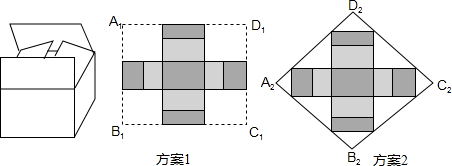
（2011•南岗区二模）在综合实践课上，小明要用如图所示的矩形硬纸板做一个装垃圾的无盖纸盒．已知这张矩形硬纸板ABCD边AB的长是40cm，边AD的长是20cm，裁去角上四个小正方形之后，就可以折成一个无盖纸盒．设这个无盖纸盒的底面矩形EFMN的面积是y（单位：cm2），纸盒的高是x（单位：cm）．
在综合实践课上，小明要用如图所示的矩形硬纸板做一个装垃圾的无盖纸盒．已知这张矩形硬纸板ABCD边AB的长是40cm，边AD的长是20cm，裁去角上四个小正方形之后，就可以折成一个无盖纸盒．设这个无盖纸盒的底面矩形EFMN的面积是y（单位：cm2），纸盒的高是x（单位：cm）．