题目内容
在综合实践课上,小明要用如图所示的矩形硬纸板做一个装垃圾的无盖纸盒.已知这张矩形硬纸板ABCD边AB的长是40cm,边AD的长是20cm,裁去角上四个小正方形之后,就可以折成一个无盖纸盒.设这个无盖纸盒的底面矩形EFMN的面积是y(单位:cm2),纸盒的高是x(单位:cm).(1)求出y与x之间的函数关系式(不要求写出自变量x的取值范围);
(2)根据老师要求,小明做的无盖纸盒的高x不能超过宽EF且纸盒的底面矩形EFMN的面积y等于300cm2,求纸盒高的最大整数值x是多少cm?

【答案】分析:(1)根据已知得出NE=AB-2x=40-2x,EF=BC-2x=20-2x,即可得出y与x之间的函数关系式;
(2)根据纸盒的底面矩形EFMN的面积y等于300cm2,求出x即可得出答案.
解答:解:(1)在矩形EFMN中,NE=AB-2x=40-2x,EF=BC-2x=20-2x,
y=(40-2x)(20-2x),
即:y=4x 2-120x+800;
(2)依据题意得出:4x 2-120x+800=300,
解得:x1=5,x2=25,
∵x≤EF,∴x≤20-2x,
即x≤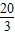 ,
,
即纸盒高的最大整数值为6cm.
点评:此题主要考查了二次函数的应用以及一元二次方程的应用,根据已知得出NE=AB-2x=40-2x,EF=BC-2x=20-2x,是解题关键.
(2)根据纸盒的底面矩形EFMN的面积y等于300cm2,求出x即可得出答案.
解答:解:(1)在矩形EFMN中,NE=AB-2x=40-2x,EF=BC-2x=20-2x,
y=(40-2x)(20-2x),
即:y=4x 2-120x+800;
(2)依据题意得出:4x 2-120x+800=300,
解得:x1=5,x2=25,
∵x≤EF,∴x≤20-2x,
即x≤
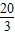 ,
,即纸盒高的最大整数值为6cm.
点评:此题主要考查了二次函数的应用以及一元二次方程的应用,根据已知得出NE=AB-2x=40-2x,EF=BC-2x=20-2x,是解题关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
 (2011•南岗区二模)在综合实践课上,小明要用如图所示的矩形硬纸板做一个装垃圾的无盖纸盒.已知这张矩形硬纸板ABCD边AB的长是40cm,边AD的长是20cm,裁去角上四个小正方形之后,就可以折成一个无盖纸盒.设这个无盖纸盒的底面矩形EFMN的面积是y(单位:cm2),纸盒的高是x(单位:cm).
(2011•南岗区二模)在综合实践课上,小明要用如图所示的矩形硬纸板做一个装垃圾的无盖纸盒.已知这张矩形硬纸板ABCD边AB的长是40cm,边AD的长是20cm,裁去角上四个小正方形之后,就可以折成一个无盖纸盒.设这个无盖纸盒的底面矩形EFMN的面积是y(单位:cm2),纸盒的高是x(单位:cm). ,高为8
,高为8 ,高为8
,高为8 在综合实践课上,小明要用如图所示的矩形硬纸板做一个装垃圾的无盖纸盒.已知这张矩形硬纸板ABCD边AB的长是40cm,边AD的长是20cm,裁去角上四个小正方形之后,就可以折成一个无盖纸盒.设这个无盖纸盒的底面矩形EFMN的面积是y(单位:cm2),纸盒的高是x(单位:cm).
在综合实践课上,小明要用如图所示的矩形硬纸板做一个装垃圾的无盖纸盒.已知这张矩形硬纸板ABCD边AB的长是40cm,边AD的长是20cm,裁去角上四个小正方形之后,就可以折成一个无盖纸盒.设这个无盖纸盒的底面矩形EFMN的面积是y(单位:cm2),纸盒的高是x(单位:cm).