题目内容
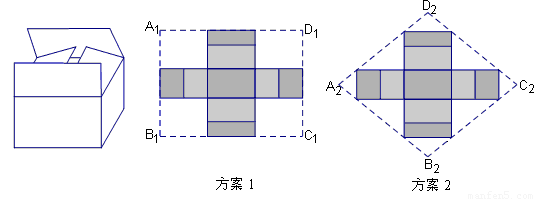
知识背景:恩施来凤有一处野生古杨梅群落,其野生杨梅是一种具特殊价值的绿色食品.在当地市场出售时,基地要求“杨梅”用双层上盖的长方体纸箱封装(上盖纸板面积刚好等于底面面积的2倍,如图)(1)实际运用:如果要求纸箱的高为0.5米,底面是黄金矩形(宽与长的比是黄金比,取黄金比为0.6),体积为0.3立方米.
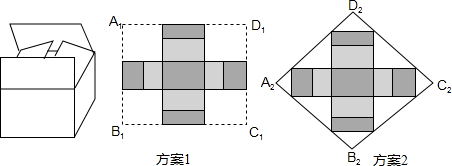
①按方案1(如图)做一个纸箱,需要矩形硬纸板A1B1C1D1的面积是多少平方米?
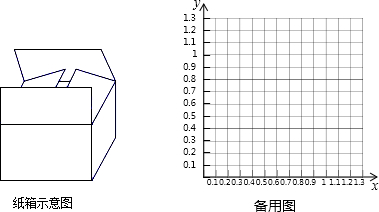
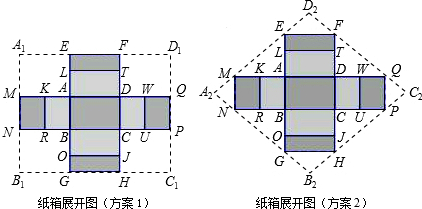
②小明认为,如果从节省材料的角度考虑,采用方案2(如图)的菱形硬纸板A2B2C2D2做一个纸箱比方案1更优,你认为呢?请说明理由.
(2)拓展思维:北方一家水果商打算在基地购进一批“野生杨梅”,但他感觉(1)中的纸箱体积太大,搬运吃力,要求将纸箱的底面周长、底面面积和高都设计为原来的一半,你认为水果商的要求能办到吗?请利用函数图象验证.
分析:(1)①利用宽与长的比是黄金比,取黄金比为0.6,假设底面长为x,宽就为0.6x,再利用图形得出QM=
+0.5+1+0.5+
=3,FH=0.3+0.5+0.6+0.5+0.3=2.2,进而求出即可;
②根据菱形的性质得出,对角线乘积的一半绝对小于矩形边长乘积即可得出答案;
(2)根据相似三角形的性质面积比等于相似比的平方得出即可.
| 1 |
| 2 |
| 1 |
| 2 |
②根据菱形的性质得出,对角线乘积的一半绝对小于矩形边长乘积即可得出答案;
(2)根据相似三角形的性质面积比等于相似比的平方得出即可.
解答:解:(1)①∵纸箱的高为0.5米,底面是黄金矩形(宽与长的比是黄金比,取黄金比为0.6),体积为0.3立方米,
∴假设底面长为x,宽就为0.6x,
∴体积为:0.6x•x•0.5=0.3,
解得:x=1,
∴AD=1,CD=0.6,
DW=KA=DT=JC=0.5,FT=JH=
CD=0.3,
WQ=MK=
AD=
,
∴QM=
+0.5+1+0.5+
=3,
FH=0.3+0.5+0.6+0.5+0.3=2.2,
∴矩形硬纸板A1B1C1D1的面积是3×2.2=6.6(平方米);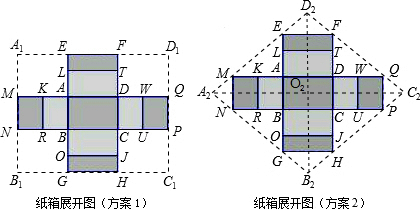
②
如图,连接A2C2,B2D2相交于O2,
设△D2EF中EF边上的高为h1,△A2NM中NM边上的高为h2,
由△D2EF∽△D2MQ得,
=
,
解得:h1=0.4,
同理可得出:h 2=
,
∴A2C2=
,B2D2=3,
又四边形A2B2C2D2是菱形,
故S菱形A2B2C2D2=5.625(平方米),
∴从节省材料的角度考虑,
采用方案2(如图)的菱形硬纸板A2B2C2D2做一个纸箱比方案1更优.
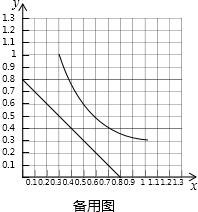
(2)水果商的要求不能办到.
设底面的长与宽分别为 x、y,
则 x+y=0.8,xy=0.3,
即 y=0.8-x 和 y=
,
在 y=0.8-x 中,
当x=0.8,y=0,x=0,y=0.8,
在y=
中,
当x=1,y=0.3,
x=0.3,y=1,画出其图象如图所示.
因为两个函数图象无交点,故水果商的要求无法办到.
∴假设底面长为x,宽就为0.6x,
∴体积为:0.6x•x•0.5=0.3,
解得:x=1,
∴AD=1,CD=0.6,
DW=KA=DT=JC=0.5,FT=JH=
| 1 |
| 2 |
WQ=MK=
| 1 |
| 2 |
| 1 |
| 2 |
∴QM=
| 1 |
| 2 |
| 1 |
| 2 |
FH=0.3+0.5+0.6+0.5+0.3=2.2,
∴矩形硬纸板A1B1C1D1的面积是3×2.2=6.6(平方米);

②
如图,连接A2C2,B2D2相交于O2,
设△D2EF中EF边上的高为h1,△A2NM中NM边上的高为h2,
由△D2EF∽△D2MQ得,
| h1 |
| h1+0.8 |
| 1 |
| 3 |
解得:h1=0.4,
同理可得出:h 2=
| 3 |
| 8 |
∴A2C2=
| 15 |
| 4 |
又四边形A2B2C2D2是菱形,
故S菱形A2B2C2D2=5.625(平方米),
∴从节省材料的角度考虑,
采用方案2(如图)的菱形硬纸板A2B2C2D2做一个纸箱比方案1更优.

(2)水果商的要求不能办到.
设底面的长与宽分别为 x、y,
则 x+y=0.8,xy=0.3,
即 y=0.8-x 和 y=
| 0.3 |
| x |
在 y=0.8-x 中,
当x=0.8,y=0,x=0,y=0.8,
在y=
| 0.3 |
| x |
当x=1,y=0.3,
x=0.3,y=1,画出其图象如图所示.
因为两个函数图象无交点,故水果商的要求无法办到.
点评:此题主要考查了一元二次方程的应用以及正方形性质与菱形性质等知识,根据题意得出DW=KA=DT=JC=0.5,FT=JH=
CD=0.3,WQ=MK=
AD=
是解决问题的关键.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
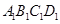 的面积是多少平方米?
的面积是多少平方米?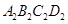 做一个纸箱比方案1更优,你认为呢?请说明理由.
做一个纸箱比方案1更优,你认为呢?请说明理由.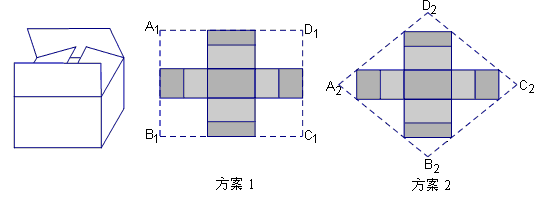
 的面积是多少平方米?
的面积是多少平方米? 做一个纸箱比方案1更优,你认为呢?请说明理由.
做一个纸箱比方案1更优,你认为呢?请说明理由.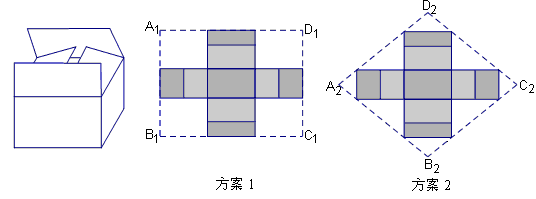
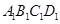 的面积是多少平方米?
的面积是多少平方米?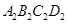 做一个纸箱比方案1更优,你认为呢?请说明理由.
做一个纸箱比方案1更优,你认为呢?请说明理由.