题目内容
如图,抛物线y=a(x+1)(x-5)与x轴的交点为M,N.直线y=kx+b与x轴交于P(-2,0),与y轴交于C.若A,B两点在直线y=kx+b上,且AO=BO=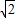 ,AO⊥BO.D为线段MN的中点,OH为Rt△OPC斜边上的高.
,AO⊥BO.D为线段MN的中点,OH为Rt△OPC斜边上的高.(1)OH的长度等于______;k=______,b=______;
(2)是否存在实数a,使得抛物线y=a(x+1)(x-5)上有一点E,满足以D,N,E为顶点的三角形与△AOB相似?若不存在,说明理由;若存在,求所有符合条件的抛物线的解析式,同时探索所求得的抛物线上是否还有符合条件的E点(简要说明理由);并进一步探索对符合条件的每一个E点,直线NE与直线AB的交点G是否总满足PB•PG<10
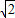 ,写出探索过程.
,写出探索过程.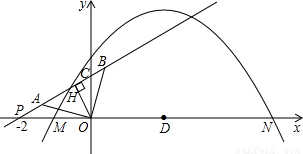
【答案】分析:(1)由已知在等腰直角三角形中解出OH的长,因直线过顶点和OH长等于点到直线距离,联立方程求出k,b;
(2)思维要严密,分两类情况:①若DN为等腰直角三角形的直角边;②若DN为等腰直角三角形的斜边.
根据相似的比例关系和几何关系,作适合的辅助线,构造垂直从而验证相似比例关系是否成立.
解答: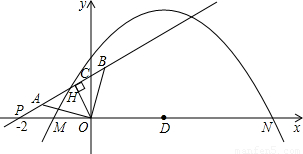 解:(1)∵直线y=kx+b过P(-2,0)?-2k+b=0…①
解:(1)∵直线y=kx+b过P(-2,0)?-2k+b=0…①
∵AO=BO=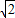 ,AO⊥BO?三角形AOB为等腰直角三角形,
,AO⊥BO?三角形AOB为等腰直角三角形,
AB=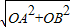 =2?∠OAB=45°?OH=OA×sin45°=1,
=2?∠OAB=45°?OH=OA×sin45°=1,
∵OH=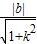 =1…②
=1…②
由①②方程解得:k=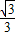 ,b=
,b=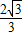 ,OH=1.
,OH=1.
(2)设存在实数a,使抛物线y=a(x+1)(x-5)上有一点E,满足以D,N,E为顶点的三角形与等腰直角△AOB相似.
∴以D,N,E为顶点的三角形为等腰直角三角形,且这样的三角形最多只有两类,一类是以DN为直角边的等腰直角三角形,另一类是以DN为斜边的等腰直角三角形.
①若DN为等腰直角三角形的直角边,则ED⊥DN.
在抛物线y=a(x+1)(x-5)中,令y=0,解得x=-1或5,则得:M(-1,0),N(5,0).
∴D(2,0),
∴ED=DN=3.
∴E的坐标为(2,3).
把E(2,3)代入抛物线解析式y=a(x+1)(x-5),得:a(2+1)(2-5)=3,解得a=- .
.
∴抛物线解析式为y=- (x+1)(x-5).
(x+1)(x-5).
即y=- x2+
x2+ x+
x+ .
.
②若DN为等腰直角三角形的斜边,
则DE⊥EN,DE=EN.
∴E的坐标为(3.5,1.5).
把E(3.5,1.5)代入抛物线解析式y=a(x+1)(x-5)得:a(3.5+1)(3.5-5)=1.5,解得a=- .
.
∴抛物线解析式为y=- (x+1)(x-5),
(x+1)(x-5),
即y=- x2+
x2+ x+
x+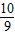 .
.
当a=- 时,在抛物线y=-
时,在抛物线y=- x2+
x2+ x+
x+ 上存在一点E(2,3)满足条件,
上存在一点E(2,3)满足条件,
如果此抛物线上还有满足条件的E点,不妨设为E′点,那么只有可能△DE′N是以DN为斜边的等腰直角三角形,
由此得E′(3.5,1.5),显然E′不在抛物线.
y=- x2+
x2+ x+
x+ 上,
上,
因此抛物线y=- x2+
x2+ x+
x+ 上没有符合条件的其他的E点.
上没有符合条件的其他的E点.
当a=- 时,同理可得抛物线y=-
时,同理可得抛物线y=- x2+
x2+ x+
x+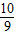 上没有符合条件的其他的E点.
上没有符合条件的其他的E点.
当E的坐标为(2,3),对应的抛物线解析式为y=- x2+
x2+ x+
x+ 时,
时,
∵△EDN和△ABO都是等腰直角三角形,
∴∠GNP=∠PBO=45°.
又∵∠NPG=∠BPO,
∴△NPG∽△BPO.
∴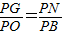 ,
,
∴PB•PG=PO•PN=2×7=14,
∴总满足PB•PG<10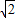 .
.
当E的坐标为(3.5,1.5),解得对应的抛物线解析式为y=- x2+
x2+ x+
x+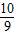 时,
时,
同理可证得:PB•PG=PO•PN=2×7=14,
∴总满足PB•PG<10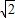 .
.
点评:此题考查在直角三角形中解题技巧,通过解方程组来求抛物线解析式,第二问探究三角形相似问题,考查思维的严密性,不要漏掉其它情况,学会分类讨论.
(2)思维要严密,分两类情况:①若DN为等腰直角三角形的直角边;②若DN为等腰直角三角形的斜边.
根据相似的比例关系和几何关系,作适合的辅助线,构造垂直从而验证相似比例关系是否成立.
解答:
 解:(1)∵直线y=kx+b过P(-2,0)?-2k+b=0…①
解:(1)∵直线y=kx+b过P(-2,0)?-2k+b=0…①∵AO=BO=
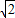 ,AO⊥BO?三角形AOB为等腰直角三角形,
,AO⊥BO?三角形AOB为等腰直角三角形,AB=
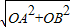 =2?∠OAB=45°?OH=OA×sin45°=1,
=2?∠OAB=45°?OH=OA×sin45°=1,∵OH=
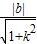 =1…②
=1…②由①②方程解得:k=
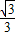 ,b=
,b=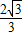 ,OH=1.
,OH=1.(2)设存在实数a,使抛物线y=a(x+1)(x-5)上有一点E,满足以D,N,E为顶点的三角形与等腰直角△AOB相似.
∴以D,N,E为顶点的三角形为等腰直角三角形,且这样的三角形最多只有两类,一类是以DN为直角边的等腰直角三角形,另一类是以DN为斜边的等腰直角三角形.
①若DN为等腰直角三角形的直角边,则ED⊥DN.
在抛物线y=a(x+1)(x-5)中,令y=0,解得x=-1或5,则得:M(-1,0),N(5,0).
∴D(2,0),
∴ED=DN=3.
∴E的坐标为(2,3).
把E(2,3)代入抛物线解析式y=a(x+1)(x-5),得:a(2+1)(2-5)=3,解得a=-
 .
.∴抛物线解析式为y=-
 (x+1)(x-5).
(x+1)(x-5).即y=-
 x2+
x2+ x+
x+ .
.②若DN为等腰直角三角形的斜边,
则DE⊥EN,DE=EN.
∴E的坐标为(3.5,1.5).
把E(3.5,1.5)代入抛物线解析式y=a(x+1)(x-5)得:a(3.5+1)(3.5-5)=1.5,解得a=-
 .
.∴抛物线解析式为y=-
 (x+1)(x-5),
(x+1)(x-5),即y=-
 x2+
x2+ x+
x+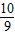 .
.当a=-
 时,在抛物线y=-
时,在抛物线y=- x2+
x2+ x+
x+ 上存在一点E(2,3)满足条件,
上存在一点E(2,3)满足条件,如果此抛物线上还有满足条件的E点,不妨设为E′点,那么只有可能△DE′N是以DN为斜边的等腰直角三角形,
由此得E′(3.5,1.5),显然E′不在抛物线.
y=-
 x2+
x2+ x+
x+ 上,
上,因此抛物线y=-
 x2+
x2+ x+
x+ 上没有符合条件的其他的E点.
上没有符合条件的其他的E点.当a=-
 时,同理可得抛物线y=-
时,同理可得抛物线y=- x2+
x2+ x+
x+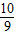 上没有符合条件的其他的E点.
上没有符合条件的其他的E点.当E的坐标为(2,3),对应的抛物线解析式为y=-
 x2+
x2+ x+
x+ 时,
时,∵△EDN和△ABO都是等腰直角三角形,
∴∠GNP=∠PBO=45°.
又∵∠NPG=∠BPO,
∴△NPG∽△BPO.
∴
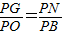 ,
,∴PB•PG=PO•PN=2×7=14,
∴总满足PB•PG<10
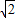 .
.当E的坐标为(3.5,1.5),解得对应的抛物线解析式为y=-
 x2+
x2+ x+
x+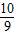 时,
时,同理可证得:PB•PG=PO•PN=2×7=14,
∴总满足PB•PG<10
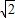 .
.点评:此题考查在直角三角形中解题技巧,通过解方程组来求抛物线解析式,第二问探究三角形相似问题,考查思维的严密性,不要漏掉其它情况,学会分类讨论.

练习册系列答案
相关题目
 如图,抛物线y=ax2+bx+c(a≠0)与x轴两交点是A(-1,0),B(3,0),则如图可知y<0时,x的取值范围是( )
如图,抛物线y=ax2+bx+c(a≠0)与x轴两交点是A(-1,0),B(3,0),则如图可知y<0时,x的取值范围是( )| A、-1<x<3 | B、3<x<-1 | C、x>-1或x<3 | D、x<-1或x>3 |
 26、已知:如图,抛物线C1,C2关于x轴对称;抛物线C1,C3关于y轴对称.抛物线C1,C2,C3与x轴相交于A、B、C、D四点;与y相交于E、F两点;H、G、M分别为抛物线C1,C2,C3的顶点.HN垂直于x轴,垂足为N,且|OE|>|HN|,|AB|≠|HG|
26、已知:如图,抛物线C1,C2关于x轴对称;抛物线C1,C3关于y轴对称.抛物线C1,C2,C3与x轴相交于A、B、C、D四点;与y相交于E、F两点;H、G、M分别为抛物线C1,C2,C3的顶点.HN垂直于x轴,垂足为N,且|OE|>|HN|,|AB|≠|HG| 如图,抛物线交x轴于点A(-2,0),点B(4,0),交y轴于点C(0,4).
如图,抛物线交x轴于点A(-2,0),点B(4,0),交y轴于点C(0,4). 以P为圆心的圆经过点A,并且与直线BM相切?若存在,求出点P的坐标;若不存在,请说明理由.
以P为圆心的圆经过点A,并且与直线BM相切?若存在,求出点P的坐标;若不存在,请说明理由. .点C是点A关于点B的对称点,点F是线段BC的中点,直线l过点F且与y轴平行.直线y=-x+m过点C,交y轴于D点.
.点C是点A关于点B的对称点,点F是线段BC的中点,直线l过点F且与y轴平行.直线y=-x+m过点C,交y轴于D点.